---

Introduction

Molecules can be regarded as sets of nuclei embedded in the negative charge cloud generated by their electrons. The shape and size of this cloud changes from one electronic state to another and, in a given state, with the particular arrangement (conformation) of the nuclei. However, not all states and nuclear conformations present the same interest.

Considering the electronic states, it is specially relevant the ground state in which most chemical processes occur. Among all the possible nuclear arrangements in this state, the equilibrium conformation is basic because, in the unperturbed stable molecule, nuclei usually tend to remain around this position.

The features of the electron cloud are completely determined by the electron density, 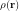,which gives the probability per volume unit (density of probability) of finding any electron at every point of space.

Electron density and its functionals are taking an increasingly central role in the conceptual and practical development of the theoretical chemistry. Indeed, this is due in part to the wide acceptation of the density functional theory (DFT), but density has intrinsic merits to occupy this place.

Electron density is an observable that can be experimentally measured and which determines all the remaining local one-electron observables. Though this is interesting because many of these observables play relevant roles, even more important is the fact that density determines all the chemical forces and hence the chemical behavior. This fact, which sets the study of electron density as the central problem of chemistry, deserves a short digression.

In the Born-Oppenheimer approximation (the paradigm in the study of the molecular structure) the electronic energy is the potential energy for the movement of the nuclei and, as a consequence, the components of the force acting on a nucleus are the derivatives of the electron energy with respect to the coordinates of that nucleus (multiplied by -1). The Hellmann-Feynman (electrostatic) theorem states that these derivatives are equal to the components of the electrostatic force generated by the electron cloud plus the remaining nuclei. Thus, the forces can be obtained in two ways: from the electronic energy and its derivatives or from the electron density using classical electrostatics. The first way is expensive and hardly provides chemical insight. The second one is very cheap to apply and plenty of chemical insight.

Nonetheless, in spite of the fact that electrostatic theorem is known more than sixty years ago, the possibilities that it opens have been not exploited, and today the theorem is mostly regarded as a scientific curiosity. There have been two main reasons for this. The first one is that the fulfillment of the theorem requires high quality densities. In particular, it leads to disastrous results for densities computed with commonly used poor basis sets, whereas energy is less sensitive to the quality of the basis set. The second reason comes from the fact that, for extracting chemical information from the theorem, one needs a representation of the density that brings insight to chemists.

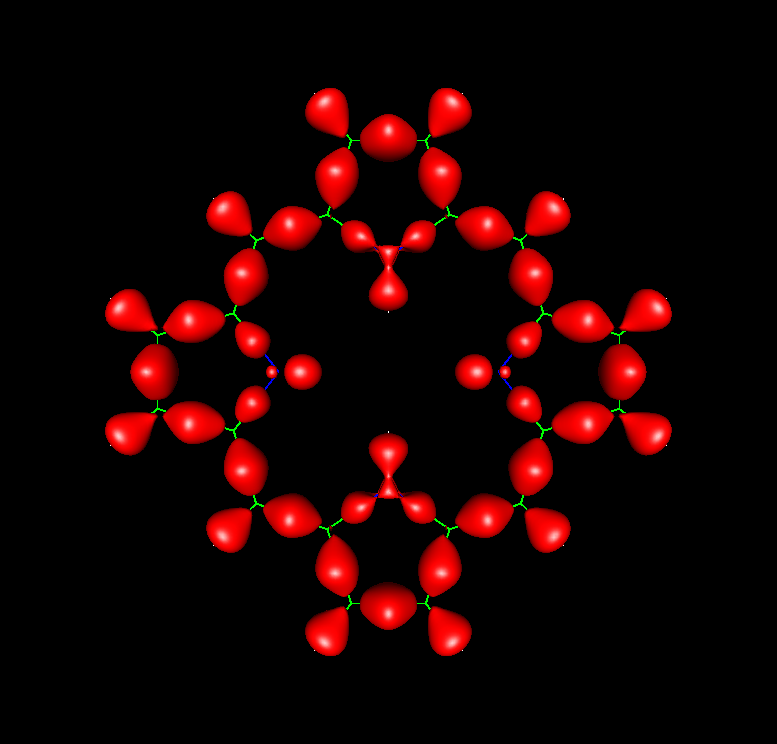
These reasons no longer hold. As it has been reently proved, densities computed with good Slater basis sets, and with very high quality Gaussian basis sets too, fulfill the electrostatic theorem with an accuracy that is sufficient for most quantitative applications and, a fortiori, for the qualitative ones. Moreover, it has been also reported a representation of the density aimed to retain the identity of the atoms in a molecule as much as possible and that, in turn, facilitates the application of the electrostatic theorem.

Basically, in this method the molecular density is partitioned into minimally deformed pseudoatomic densities, which are achieved by assigning to each atom the charge distributions centered on its nucleus plus the part of the two-center ones closer to it. This partition ensures that atomic densities exactly reproduce (on summation) the whole density and, furthermore, that pseudoatomic densities can be accurately represented in terms of rapidly convergent expansions in regular harmonics times radial factors.

The method can be applied to densities calculated with Slater or Gaussian basis sets and has been implemented in the DAM (Slater) and G-DAM (Gaussian) programs.

This representation was originally intended as an aid for the calculation of several functionals of the electron density such as the molecular electrostatic potential, molecular force field, forces on nuclei, etc, and it was proved to be very useful for this purpose. The method was also applied to the analysis of binding forces and to the calculation of bonding energies from the density in diatomics, as well as to the explanation of the rotational barrier of ethane in terms of the density.

These studies render evident that, combining this representation of the density with the electrostatic theorem, basic concepts of chemistry can be regarded from a novel perspective that may help to build a bridge between electron density and the classical notions of the empirical structural chemistry. The exploration of this possibility is the aim of the content of this web page. Readers interested in how the deformed atoms in molecules method describes the density and how the electrostatic theorem can be combined with this description may get further information by clicking here.

The formal developments of this method are detailed in the references listed in the bibliography and its basic ideas are clarified herein with an illustrative example.

---