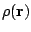 |
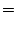 |
 |
|
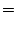 |
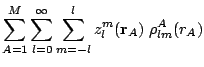 |
(1) |
The method of Deformed Atoms in Molecules (DAM) proceeds in two steps. First, the whole density of the molecule is partitioned into atomic contributions (that will be called pseudoatomic densities) following two partition criteria:
Once the pseudoatomic densities have been determined in a given system, the second step consists in the expansion of every atomic contribution in regular harmonics times radial factors centered in the corresponding nucleus. This process yields the molecular density as:
 ,
,  ... label the nuclei, and
... label the nuclei, and  ,
, 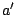 ,
, 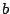 ,
, 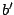 label the subsets of the
basis functions,
label the subsets of the
basis functions, 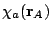 ,
, 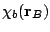 ,
... centered respectively at
,
... centered respectively at 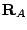 ,
, 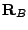 ,...; and
,...; and 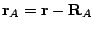 ,
, 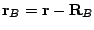 . The
regular spherical harmonics defined as:
. The
regular spherical harmonics defined as:
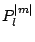 are the
associated Legendre functions.
are the
associated Legendre functions. 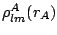 , are
accurately computed and fitted to piecewise analytical functions. DAM
carries out this process in a very efficient way for Slater (DAM
program) and Gaussian (G-DAM) functions.
, are
accurately computed and fitted to piecewise analytical functions. DAM
carries out this process in a very efficient way for Slater (DAM
program) and Gaussian (G-DAM) functions. This representation of the density gives a very detailed
description of how density is arranged around each nucleus, which can be
visualized, for instance, by depicting contour lines for every single
term of the expansion. In this respect, it is important to recall that
these expansions are, by construction, very rapidly convergent, so that
plots of succesive terms may require very different contour values to be
visible. Thus, spherical terms (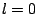 ) are, without any
exception, very much larger than terms corresponding to deformations (
) are, without any
exception, very much larger than terms corresponding to deformations (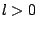 ). Even, among these
latter, dipole (
). Even, among these
latter, dipole (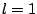 ) and quadrupole (
) and quadrupole (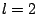 ) are of the same
order of magnitude and, usually, considerably larger than the following
terms in the expansion (octapoles, hexadecapoles, ...), which can be
neglected in many cases. The following pictures illustrate the contour
lines in the molecular plane for the first terms of the atomic
expansions in ethylene.
) are of the same
order of magnitude and, usually, considerably larger than the following
terms in the expansion (octapoles, hexadecapoles, ...), which can be
neglected in many cases. The following pictures illustrate the contour
lines in the molecular plane for the first terms of the atomic
expansions in ethylene.
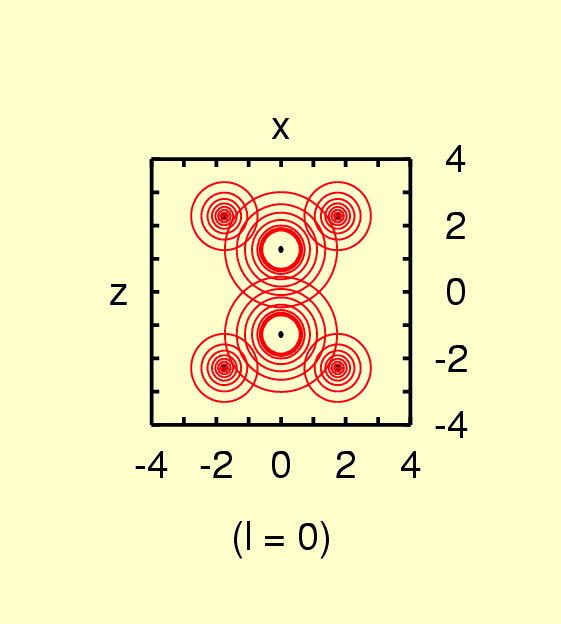
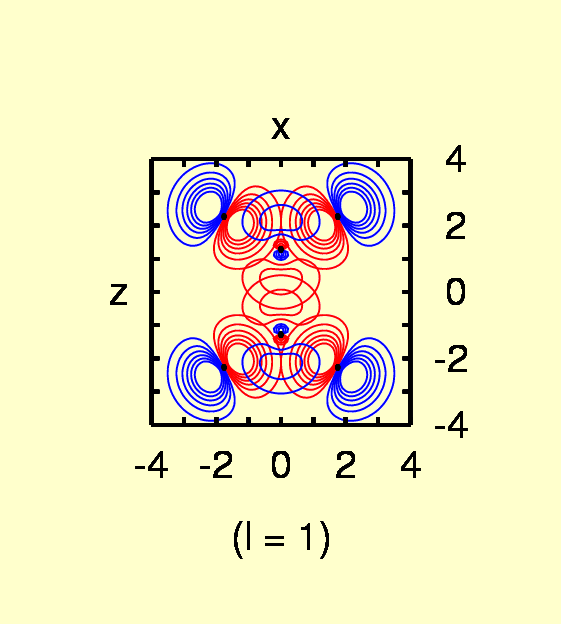
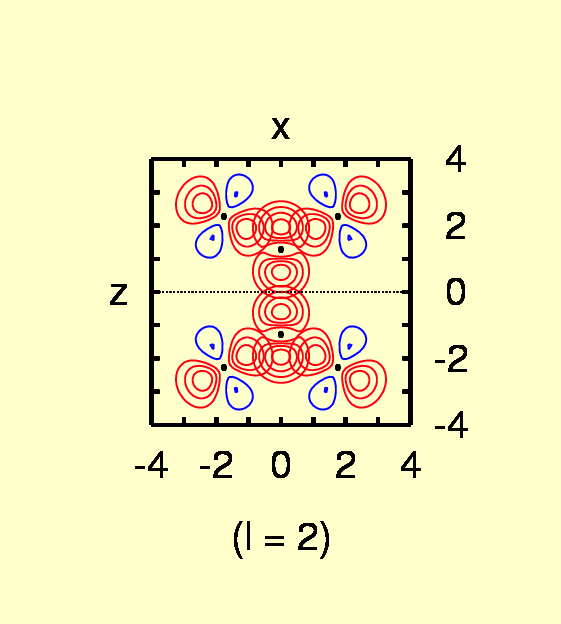
(Contours: for l = 0, from 0.05 to 0.4 in steps of
0.05; l = 1, from -0.03
to 0.03 in steps of 0.005; l = 2,from
-0.03 to 0.03 in steps of 0.005 for C, from -0.0025 to 0.0075 in steps
of 0.0025 for H)
The convergence of the expansion can be examined by comparing
the contour lines of the exact density with those corresponding to
succesive truncations. Usually, truncation at 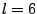 is sufficient to
reach an accuracy of four decimal places in the whole density.
Nonetheless, both DAM and G-DAM programs are prepared to work with
expansions up to
is sufficient to
reach an accuracy of four decimal places in the whole density.
Nonetheless, both DAM and G-DAM programs are prepared to work with
expansions up to 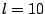 .
.
The whole density, atomic densities and every component of
their representations can be visualized by depicting their constant
value contour surfaces in physical space (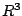 ). Moreover, drawing
together several of these surfaces, one can obtain very complete and
meaningful pictures of the electronic cloud or its components. In this
way, it is very illustrative to compare the pictures of the whole
molecular density with the summation of the spherical terms of the
atomic densities. In the following figures, the full electon density (left plates)
and the sum of spherical terms
(right plates) are depicted for water, acetic acid, benzene
and diborane:
). Moreover, drawing
together several of these surfaces, one can obtain very complete and
meaningful pictures of the electronic cloud or its components. In this
way, it is very illustrative to compare the pictures of the whole
molecular density with the summation of the spherical terms of the
atomic densities. In the following figures, the full electon density (left plates)
and the sum of spherical terms
(right plates) are depicted for water, acetic acid, benzene
and diborane:
Water
Acetic acid
Benzene
Diborane
As it can be seen in these examples, the close similarity between these
two types of pictures shows again that the molecular density is largely
dominated by the spherical parts of its constituent atoms.
Let us comment now the consequences of the application of the electrostatic theorem in this context. As it has been mentioned above, the theorem states that the force acting on a nucleus is equal to the electrostatic force exerted on it by the electron cloud and by the other nuclei. With the molecular cloud partitioned into atomic contributions, the electrostatic force on the nucleus can be written as:
The first contribution is the self-pulling force, namely, the
force exerted on a nucleus 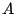 by its own cloud. The
second term is the external force, exerted by the clouds and nuclei of
the remaining atoms.
by its own cloud. The
second term is the external force, exerted by the clouds and nuclei of
the remaining atoms.
In this line of thought, it is essential to know how these
contributions are affected by the spherical, dipole, and succesive terms
of the atomic expansions.
In case of the self-pulling force, symmetry considerations are
sufficient to see that the only term in the expansion of 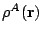 giving a
non-vanishing
giving a
non-vanishing
contribution is the dipole term (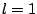 ). In case of the
external force, all expansion terms of any
). In case of the
external force, all expansion terms of any 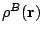 do
contribute, the point here being their magnitude. As stressed above,
spherical terms of the
do
contribute, the point here being their magnitude. As stressed above,
spherical terms of the 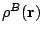 density
are largely dominant, and in consequence the external force on a given
nucleus will be mainly determined by the balance between the forces
generated by the nuclei and spherical clouds of the remaining atoms.
density
are largely dominant, and in consequence the external force on a given
nucleus will be mainly determined by the balance between the forces
generated by the nuclei and spherical clouds of the remaining atoms.
Neglecting the effects of the small deformation terms, one can write:
The second term in eq(5)
is part of the electron charge associated to the cloud of atom 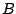 and therefore, in neutral
atoms or in cations, the net effect of external forces is repulsive. For
anions, this effect is attractive at long distances but changes to
repulsive at short ones.
and therefore, in neutral
atoms or in cations, the net effect of external forces is repulsive. For
anions, this effect is attractive at long distances but changes to
repulsive at short ones.
It is very illustrative to consider how the forces between a
pair of atoms or ions strictly spherical would be. In this case, the
self-pulling force is obviously zero and only external forces remain. As
proved before, these forces are repulsive for couples of neutral atoms,
an atom and a cation or pairs of cations. In case of a system
consisting in a cation (or a neutral atom) and an anion, the force on
the anion nucleus will be always repulsive (at all distances) whereas
the force on the cation nucleus will be attractive at long distances and
repulsive at short ones. Note that none of these couples can conform a
stable system. In order to form a stable system, densities cannot have
spherical symmetry. In other words, density
deformations are essential for the appearance of attractive forces.