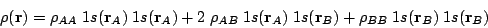 |
(1) |
In a LCAO calculation of H2 carried out with a minimal basis set, the density results:
where 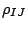 are
the elements of
the density matrix,
are
the elements of
the density matrix,
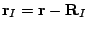 ,
,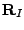 stands for the position of the nuclei
stands for the position of the nuclei 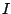 (
(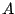 or
or 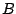 ), and
), and
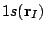 is
either a
is
either a 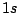 STO or the corresponding
combination of Gaussian primitives.
STO or the corresponding
combination of Gaussian primitives.
The first and third terms in (1)
contain the spherical charge distributions,
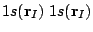 centered at the nuclei
centered at the nuclei 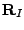 .
The second term
has the two-center charge distribution,
.
The second term
has the two-center charge distribution,
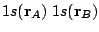 extending along the internuclear axis.
extending along the internuclear axis.
Depicting the values of these distributions along
the internuclear axis one has:
The one-center contributions to the density are:
The two-center contributions are obtained after partitioning the two-center distribution into two minimally deformed fagments:
This partitioning is illustrated in the next
figure, where the full distribution,
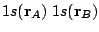 and the
and the
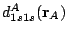 and
and 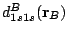 fragments have been plotted along the internuclear axis:
fragments have been plotted along the internuclear axis:
The two-center contributions are:
The 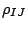 elements of the
density matrix can be obtained with different methods. Taking
elements of the
density matrix can be obtained with different methods. Taking 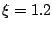 and
and
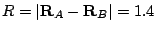 au,
and employing the VB, RHF and CI methods for
au,
and employing the VB, RHF and CI methods for 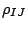 one
obtains the
following pictures of
one
obtains the
following pictures of 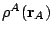 ,
, 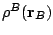 , and
, and 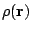 along the
internuclear axis:
along the
internuclear axis:
The last step in the method is the expansion of
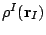 in
spherical harmonics centered at
in
spherical harmonics centered at 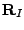 times radial
factors:
times radial
factors:
This expansion is illustrated in the following
figures by drawing the values of the first terms along the internuclear
axis. The terms with 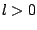 have
been multiplied by
10 for clarity.
have
been multiplied by
10 for clarity.