Desde el punto de vista de la mecánica cuántica, para estudiar un sistema que presenta una perturbación externa (como puede ser la perturbación producida por la radiación electromagnética sobre los átomos o moléculas, y que puede dar lugar a la absorción o a la emisión de un fotón) hay que resolver la ecuación de Schrödinger dependiente del tiempo1:
Utilizaremos para ello un tratamiento aproximado, válido en el caso de que se cumplan los siguientes supuestos:
Supondremos que la perturbación
![]() tiene lugar a partir de un
tiempo inicial
tiene lugar a partir de un
tiempo inicial ![]() y actúa hasta un
tiempo
y actúa hasta un
tiempo ![]() . Entonces, el Hamiltoniano
del sistema es:
. Entonces, el Hamiltoniano
del sistema es:
De esta forma, la ecuación de Schrödinger dependiente del tiempo
En general
![]() es un operador que conmuta
con
es un operador que conmuta
con ![]() , luego
, luego
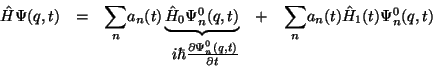
Si hacemos lo mismo en el primer término, obtenemos:
![\begin{displaymath} i\hbar \frac{\partial \Psi (q,t)}{\partial t}=i\hbar \frac{\... ...0}(q,t)}{\partial t}+\Psi _{n}^{0}(q,t)\frac{da_{n}}{dt}\right]\end{displaymath}](img23.gif)
Luego, sustituyendo en la ecuación de Schrödinger dependiente del tiempo y simplificando:
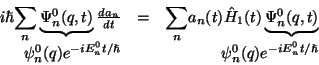
Con el fin de simplificar la notación, tomamos
![]() . Esta última
ecuación aun depende de las coordenadas de posición y espín (que
hemos denotado por
. Esta última
ecuación aun depende de las coordenadas de posición y espín (que
hemos denotado por ![]() ). Para simplificarla,
multiplicaremos ambos miembros por
). Para simplificarla,
multiplicaremos ambos miembros por
![]() e integraremos en
e integraremos en
![]() (es decir, proyectaremos sobre
(es decir, proyectaremos sobre
![]() ):
):
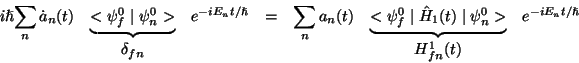
Es decir,
donde hemos definido la frecuencia angular
Formalmente, podemos integrar la ecuación anterior desde el
inicio de la perturbación (![]() )
hasta un tiempo
)
hasta un tiempo ![]()
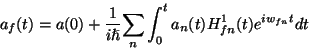
¡Nótese que en esta ecuación es necesario conocer todos los
coeficientes ![]() para poder
obtener la integral, es decir
para poder
obtener la integral, es decir ![]() !
!
Sin embargo, en este caso podemos hacer una aproximanción simple que nos permitirá obtener una solución:
![\includegraphics[ scale=0.4]{fig21.1.ps}](img41.gif)
Luego, en la suma anterior podemos quedarnos sólo con el
término ![]() -esimo
-esimo
Nótese que en esta aproximación sólo se tienen en cuenta
mecanismos directos o de primer orden (1 en la figura) que pueden
inducir la transición desde el estado inicial ![]() a un estado
a un estado ![]() , mientras que no se contemplan
mecanismos indirectos o de mayor orden, como los
representados en la siguiente figura
, mientras que no se contemplan
mecanismos indirectos o de mayor orden, como los
representados en la siguiente figura
![\includegraphics[]{fig21.2.ps}](img44.gif)
Una vez que cesa la perturbación (es decir, para
![]() y
y
![]() ), tendremos
), tendremos
Luego la función de estado después de ![]() es, de acuerdo con la expansión de
es, de acuerdo con la expansión de ![]()
En resumen, la función de onda del sistema se puede expresar
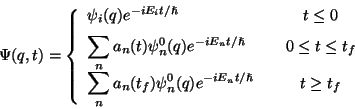
Si antes de iniciarse la perturbación ![]() realizásemos una medida de la energía del
sistema, obtendriamos con total seguridad
realizásemos una medida de la energía del
sistema, obtendriamos con total seguridad ![]() . Si realizamos una medida de la energía después
de cesar la perturbación (
. Si realizamos una medida de la energía después
de cesar la perturbación (![]() ),
podemos obtener cualquiera de las energías de los estados
estacionarios
),
podemos obtener cualquiera de las energías de los estados
estacionarios ![]() con una
probabilidad dada por el cuadrado del módulo del coeficiente
del desarrollo, es decir,
con una
probabilidad dada por el cuadrado del módulo del coeficiente
del desarrollo, es decir,
Se dice que la perturbación ha inducido la transición desde el
estado inicial ![]() a uno de los estados
a uno de los estados
![]() . Si
. Si ![]() es
la energía que se obtiene después de realizar una medida de
la energía, entonces la medida hace que la función de estado
cambie de
es
la energía que se obtiene después de realizar una medida de
la energía, entonces la medida hace que la función de estado
cambie de ![]() a
a
![]() [reducción de la función de onda].
[reducción de la función de onda].
Otra conclusión importante es que si el elemento de matriz de
la interacción (perturbación) entre el estado ![]() y el estado
y el estado ![]() ,
, ![]() es nulo, entonces la probabilidad de
transición también se anula. Es decir, a partir de los
elementos de matriz
es nulo, entonces la probabilidad de
transición también se anula. Es decir, a partir de los
elementos de matriz
![]() podemos obtener las REGLAS DE SELECCIÓN,
que indican aquellas transiciones que son prohibidas
(y por tanto de probabilidad de transición nula).
podemos obtener las REGLAS DE SELECCIÓN,
que indican aquellas transiciones que son prohibidas
(y por tanto de probabilidad de transición nula).
Nótese que si
![]() es nulo, la probabilidad es
nula REGLA
DE SELECCIÓN.
es nulo, la probabilidad es
nula REGLA
DE SELECCIÓN.
En esta sección vamos a estudiar el caso que más nos interesa, la interacción entre la radiación y la materia. Asi, con el fin de simplificar los desarrollos, consideraremos los siguientes casos:
La energía potencial de interacción entre un sistema de partículas cargadas y el campo eléctrico, viene dada por
donde
![]() es el vector momento
dipolar, y hemos despreciado términos de mayor orden a la vez que
consideramos la carga total del sistema nula (sistema neutro).
Por tanto, en una primera aproximación, esta expresión se
corresponde con el hamiltoniano de interacción
es el vector momento
dipolar, y hemos despreciado términos de mayor orden a la vez que
consideramos la carga total del sistema nula (sistema neutro).
Por tanto, en una primera aproximación, esta expresión se
corresponde con el hamiltoniano de interacción
![]() .
.
Para el caso de radiación monocromática polarizada en un plano, la dependencia con el tiempo del campo eléctrico es cosinusoidal, es decir, la interacción vendrá dada por
Para el caso de radiación plano-polarizada desplazándose en la
dirección del eje z, la componente ![]() del momento
dipolar es
del momento
dipolar es
Por tanto, la parte del Hamiltoniano, y que consideramos una pequeña perturbación, es
Y, de acuerdo con la teoría de las perturbaciones dependiente del tiempo que hemos visto
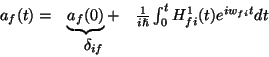
donde
![\begin{displaymath} \begin{array}{ccc} =\delta _{if}-\frac{E_{0x}}{2i\hslash }<... ...e^{i[w_{fi}-w]t}-1}{i(w_{fi}-w)}}\right]\ & A & B\end{array}\end{displaymath}](img73.gif)
Luego ![]() es prácticamente
nulo2
excepto si
es prácticamente
nulo2
excepto si
![]() .
.
![\includegraphics[]{fig24.1.eps}](img85.gif)
La principal consecuencia es que la transición inducida por la radiación es un fenómeno de resonancia. Nótese que el tratamiento que realizamos no es una demostración de que se absorbe o emite un fotón. Un tratamiento riguroso requiere la aplicación de la teoría cuántica de campos.
Para la emisión tendremos:
![]()
![\includegraphics[ scale=0.7]{fig24.2.eps}](img88.gif)
Analogamente para la absorción:
![]()
![\includegraphics[ scale=0.6]{fig24.3.eps}](img91.gif)
Nos centraremos en el proceso de absorción, para el cual
![]() . Para este caso, la probabilidad
de que se produzca la transición
. Para este caso, la probabilidad
de que se produzca la transición
![]() será:
será:
Siendo (
![]() )(
)(
![]() )=
)=
![]()
En el caso en el que la densidad de radiación no sea
monocromática debemos sustituir la densidad de radiación
![]() por una distribución continua
por una distribución continua
![]()
A continuación vamos a intentar simplificar esta ecuación,
realizando la integral. Para ello, consideraremos el
comportamiento de integrando, es decir de la función
![]() . Ésta
toma valores apreciables cuando
. Ésta
toma valores apreciables cuando
![]() , es decir, cuando
, es decir, cuando
![]() Por tanto, no
cometemos ningún error si sustituimos el límite inferior de 0 a
Por tanto, no
cometemos ningún error si sustituimos el límite inferior de 0 a
![]() . Con el cambio
. Con el cambio
![]() , tenemos
, tenemos
![]() , Y
, Y
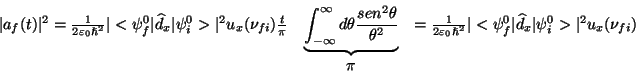
Esta expresión esta escrita en el S.I.4
La principal consecuencia que podemos obtener es que la probabilidad de que una molécula realice una transición del estado inicial i al estado f después de haber sido iluminada durante un tiempo t, viene dada por:
Para obtener la probabilidad de que se produzca emisión inducida (estimulada) por la radiación, se deberá intercambiar i por j. Así se llega a la misma expresión, luego:
Sin embargo, para un sistema macroscópico tendremos:
Las expresiones anteriores son válidas pra radiación polarizada en un plano (y policromática o blanca). Para el caso general de radiación isótropa también tendremos contribuciones debidas a los términosen las direcciones y,z. Para radiación isótropa, la densidad de radiación por unidad de frecuencia tiene el valor :
Ya que al ser isótropa tenemos
Así, sustit uyendo
![]()
donde el operador momento dipolar se define
por lo que
se denomina MOMENTO DIPOLAR DE TRANSICIÓN
donde ![]() es un
operador asociado a la propiedad A. Ejemplo
es un
operador asociado a la propiedad A. Ejemplo
![]()