COEFICIENTES DE EINSTEIN: Emisión y absorción de la radiación. Emisión
espontánea.
El tratamiento semiclásico que hemos visto tiene el defecto de que
no predice la EMISIÓN ESPONTÁNEA. Según el resultado anterior si no
hay perturbación externa (en nuestro caso radiación electromagnética)
el sistema permanecerá en el estado inicial. En efecto, si no existe
radiación, tenemos
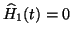 y, por tanto
y, por tanto
Si el átomo o molécula se encuentra inicialmente en el estado estacionario
i, entonces
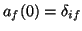 . Así, el sistema permanecerá
siempre en el estado inicial i, ya que la probabilidad de transición
a cualquier otro estado, sea absorbiendo o emitiendo un fotón, es
nula
. Así, el sistema permanecerá
siempre en el estado inicial i, ya que la probabilidad de transición
a cualquier otro estado, sea absorbiendo o emitiendo un fotón, es
nula
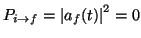 . Sin embargo,
experimentalmente se observa que los átomos y moléculas en estados
excitados radian energía espontáneamente sin necesidad de perturbación,
pasando a estados más bajos en energía.
. Sin embargo,
experimentalmente se observa que los átomos y moléculas en estados
excitados radian energía espontáneamente sin necesidad de perturbación,
pasando a estados más bajos en energía.
Esquemáticamente podemos representar los procesos de emisión y absorción
entre dos estados i y f en un diagrama de energías:
donde
 representa la población del estado i.
representa la población del estado i.
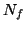 representa la población del estado f.
representa la población del estado f.
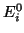 la energía del estado i, y
la energía del estado i, y
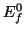 la energía del estado f.
la energía del estado f.
Para poder explicar el fenómeno de emisión espontánea es necesario
utilizar la teoría cuántica de campos (o electrodinámica cuántica).
Utilizamos un razonamiento termodinámico propuesto por Einstein en
1917 para obtener, de una forma más simple, la probabilidad de emisión
espontánea.
En el equilibrio el número de moléculas que sufren la transición
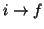 (absorción) es igual a las que sufren la transición
(absorción) es igual a las que sufren la transición
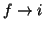 (emisión). Así, consideraremos un sistema en el que materia y radiación
están en equilibrio en una cavidad cerrada a temperatura T.1 Si suponemos cinéticas de primer orden, la velocidad de transición
del estado inicial i al final f se obtendrá a partir
de la velocidad de transición
(emisión). Así, consideraremos un sistema en el que materia y radiación
están en equilibrio en una cavidad cerrada a temperatura T.1 Si suponemos cinéticas de primer orden, la velocidad de transición
del estado inicial i al final f se obtendrá a partir
de la velocidad de transición
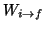 para una molécula
para una molécula
mientras que la velocidad del proceso inverso será
donde los distintos coeficientes están relacionados con las probabilidades
de absorción o emisión:
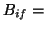 Coeficiente de Einstein de absorción.
Coeficiente de Einstein de absorción.
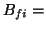 Coeficiente de emisión estimulada.
Coeficiente de emisión estimulada.
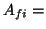 Coeficiente de emisión espontánea.
Coeficiente de emisión espontánea.
Ya hemos visto que, de acuerdo con la regla de oro de Fermi, tenemos:2
Si tenemos en cuenta las condiciones de equilibrio, tendremos:
- 1.
- Equilibrio radiación-materia.
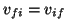 .
.
- 2.
- Equilibrio térmico de la materia a la temperatura T. Así la relación
entre las poblaciones vendrá dada por la distribución de Maxwell-
Boltzmann.
- 3.
- Equilibrio térmico de la radiación a la temperatura T. Considerando
el sistema como un cuerpo negro, la densidad de la radiación vendrá
dada por la ley de Planck del cuerpo negro.
- 4.
- Por último, como ya hemos visto, se cumple la condición de resonancia
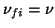 .
.
Para que se satisfagan simultáneamente las cuatro ecuaciones, tendremos,
de la primera ecuación:
Si tenemos en cuenta la segunda relación, entonces
Ecuación que, teniendo en cuenta la condición de resonancia, será
compatible con la tercera si
Así, con este tratamiento hemos vuelto a obtener que los coeficientes
de Einstein de absorción y emisión estimulada son iguales. La última
ecuación nos permite obtener el coeficiente de Einstein de emisión
espontánea. La principal consecuencia es que depende del cubo de la
frecuencia y, por tanto, la emisión estimulada será más importante
a altas frecuencias.
La existencia de emisión espontánea determina que los estados
excitados no persisten indefinidamente. Esta característica se puede
estudiar en el caso más simple de un sistema que no está sometido
a radiación electromagnética. Si f sólo puede decaer a i
tendremos, en ausencia de radiación externa:
Tiempo de vida media (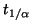 )
)
En cinética habitualmente 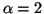
En espectroscopia 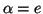
tiempo que tarda en reducirse la población al valor 1/e (36.79%)
de la población inicial.
Por último, veamos las principales características de la emisión:
- La emisión estimulada se produce en fase y colineal al fotón incidente.
- La emisión espontánea se produce en todas direcciones.
Por último, consideraremos la intensidad observada de la variación
de absorción
 . La emisión espontánea que surge de
las moléculas en estado f se envía en direcciones aleatorias.
Este es el motivo por el cual se puede observar el espectro de absorción,
pese a que la energía absorbida sea reemitida por la muestra. El efecto
neto es una absorción en la dirección del haz incidente y, cuando
se produce la reemisión, está se produce en todas las direcciones,
si bien, con intensidades diferentes. Este fenómeno se denomina difusión
o dispersión de la luz (light scattering). Si la radiación dispersada
no experimenta cambio de frecuencia con respecto a la incidente, se
denomina dispersión Rayleigh. En caso de que produzca un cambio en
la frecuencia, el efecto recibe en nombre de efecto RAMAN. Esta radiación
difundida puede observarse como un espectro de emisión que será, con
algunas reservas como veremos más adelante, complementario al espectro
de absorción.
. La emisión espontánea que surge de
las moléculas en estado f se envía en direcciones aleatorias.
Este es el motivo por el cual se puede observar el espectro de absorción,
pese a que la energía absorbida sea reemitida por la muestra. El efecto
neto es una absorción en la dirección del haz incidente y, cuando
se produce la reemisión, está se produce en todas las direcciones,
si bien, con intensidades diferentes. Este fenómeno se denomina difusión
o dispersión de la luz (light scattering). Si la radiación dispersada
no experimenta cambio de frecuencia con respecto a la incidente, se
denomina dispersión Rayleigh. En caso de que produzca un cambio en
la frecuencia, el efecto recibe en nombre de efecto RAMAN. Esta radiación
difundida puede observarse como un espectro de emisión que será, con
algunas reservas como veremos más adelante, complementario al espectro
de absorción.
Sin embargo, se puede demostrar que la emisión desde f, estimulada
por el haz de luz incidente, se propaga en la misma dirección que
el haz, disminuyendo la intensidad observada. La emisión y la absorción
estimuladas son proporcionales a la población del estado inicial de
la transición y los momentos de transición
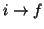 y
y
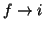 son iguales. Por tanto, la intensidad observada es proporcional a
la diferencia de poblaciones
son iguales. Por tanto, la intensidad observada es proporcional a
la diferencia de poblaciones 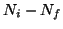 , así como a
, así como a
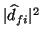 y
y 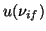 .
.
Como ya hemos visto, la velocidad de transición es proporcional a
los coeficientes de absorción y emisión de Einstein, y éstos son proporcionales
al momento dipolar de transición
Cuando está integral se anula, decimos que la transición entre los
estados i y f esta PROHIBIDA. Las condiciones entre los
números cuánticos para las cuales 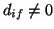 dan origen a las
reglas de selección, que especifican las transiciones
permitidas.
dan origen a las
reglas de selección, que especifican las transiciones
permitidas.
Por último, recuérdese que esta aproximación descansa en que se han
despreciado
- Procesos multifotónicos.
- Interacciones cuadrupolares (relacionadas con la variación espacial
del campo eléctrico
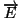 ) ya que son del orden de
) ya que son del orden de
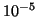 veces menos intensas que las dipolares.
veces menos intensas que las dipolares.
- La interacción del campo magnético
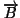 (del
orden de
(del
orden de 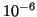 veces menos intensa).
veces menos intensa).
Aquellas transiciones de dipolo eléctrico que son prohibidas, a menudo
son transiciones permitidas por alguno de los mecanismos mencionados
(transiciones de cuadrupolo eléctrico, ...). Así, a se dice que dichas
transiciones prohibidas por dipolo eléctrico, se observan por
cuadrupolo eléctrico, etc.
Footnotes
- ...1
- Aunque esta condición de equilibrio no se da habitualmente en espectroscopia,
las probabilidades de transición son propiedades fundamentales de
la interacción radiación-materia y, por tanto, no pueden depender
de las condiciones en que se encuentre el sistema.
- ...2
- En el sistema C.G.S. la expresión se escribe
© Copyright. Alfredo Aguado y Miguel Paniagua
19-10-2004

![]() . Así, el sistema permanecerá
siempre en el estado inicial i, ya que la probabilidad de transición
a cualquier otro estado, sea absorbiendo o emitiendo un fotón, es
nula
. Así, el sistema permanecerá
siempre en el estado inicial i, ya que la probabilidad de transición
a cualquier otro estado, sea absorbiendo o emitiendo un fotón, es
nula
![]() . Sin embargo,
experimentalmente se observa que los átomos y moléculas en estados
excitados radian energía espontáneamente sin necesidad de perturbación,
pasando a estados más bajos en energía.
. Sin embargo,
experimentalmente se observa que los átomos y moléculas en estados
excitados radian energía espontáneamente sin necesidad de perturbación,
pasando a estados más bajos en energía.
![\includegraphics[ scale=0.8]{fig29.1.eps}](img5.gif)
![]() (absorción) es igual a las que sufren la transición
(absorción) es igual a las que sufren la transición
![]() (emisión). Así, consideraremos un sistema en el que materia y radiación
están en equilibrio en una cavidad cerrada a temperatura T.1 Si suponemos cinéticas de primer orden, la velocidad de transición
del estado inicial i al final f se obtendrá a partir
de la velocidad de transición
(emisión). Así, consideraremos un sistema en el que materia y radiación
están en equilibrio en una cavidad cerrada a temperatura T.1 Si suponemos cinéticas de primer orden, la velocidad de transición
del estado inicial i al final f se obtendrá a partir
de la velocidad de transición
![]() para una molécula
para una molécula
![\begin{displaymath}
\frac{N_{f}}{N_{i}}=exp\left[-\frac{E_{f}^{0}-E_{i}^{0}}{k_{B}T}\right]=exp\left[-\frac{h\nu _{fi}}{k_{B}T}\right]\end{displaymath}](img21.gif)
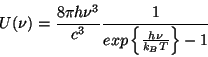
![\begin{displaymath}
u(\nu _{fi})=\frac{A_{fi}}{B_{if}exp\left[\frac{h\nu _{fi}}{K_{B}T}\right]-B_{fi}}\end{displaymath}](img25.gif)
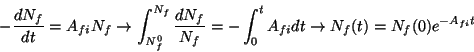
![]() )
)
![]()
![]()
![]() y
y
![]() son iguales. Por tanto, la intensidad observada es proporcional a
la diferencia de poblaciones
son iguales. Por tanto, la intensidad observada es proporcional a
la diferencia de poblaciones ![]() , así como a
, así como a
![]() y
y ![]() .
.
![]() dan origen a las
reglas de selección, que especifican las transiciones
permitidas.
dan origen a las
reglas de selección, que especifican las transiciones
permitidas.