| Constantes Fundamentales |
| Valores Internacionales recomendados
(CODATA) |
| Velocidad de la luz en el vacío |
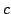 |
299 792 458 ms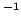 |
| Permitividad del vacío |
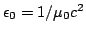 |
8.854 187 817 10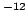 F m F m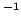 |
| Constante de Planck |
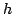 |
6.626 0693(11) 10 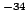 J s J s |
| |
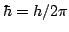 |
1.054 571 68 (18) 10 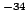 J s J s |
| Carga elemental |
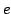 |
1.602 176 53(14) 10 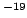 C C |
| Masa del electrón en reposo |
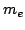 |
9.109 3826 (16) 10 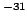 kg kg |
| Masa del protón en reposo |
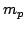 |
1.672 621 71 (29) 10 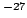 kg kg |
| Masa del neutrón en reposo |
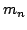 |
1.674 927 28 (29) 10 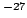 kg kg |
| Constante de masa atómica |
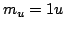 |
1.660 538 86 (28) 10 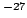 kg kg |
| Constante de Avogadro |
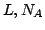 |
6.022 1415 (10) 10 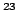 mol mol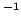 |
| Constante de Boltzmann |
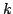 |
1.380 6505 (24) 10 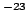 J K J K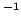 |
| Constante de los gases |
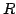 |
8.314 472 (15) J K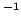 mol mol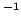 |
| Cero en la escala Celsius |
|
273.15 K |
| Radio de Bohr |
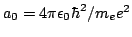 |
5.29 177 2108 (18) 10 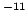 m m |
| Energía Hartree |
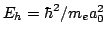 |
4.359 744 17 (75) 10 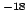 J J |
| Constante de Rydberg |
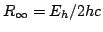 |
1.097 373 156 8525 (73) 10  m m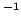 |