- 61
- Calcular la energía de repulsión nuclear para la molécula de
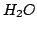 dadas las siguientes coordenadas cartesianas nucleares
dadas las siguientes coordenadas cartesianas nucleares
| Átomo |
x/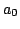 |
y/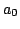 |
z/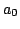 |
| |
|
|
|
| O |
0 |
0 |
0 |
| H |
-1.2 |
-1. |
0 |
| H |
1.2 |
-1. |
0 |
Solución:
Como las distancias internucleares son (en Bohr)
Análogamente, tenemos
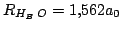 y
y
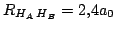 , por lo que
, por lo que
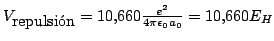
- 62
- Calcular la energía de repulsión nuclear para la molécula de
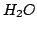 dadas las siguientes coordenadas internas nucleares
dadas las siguientes coordenadas internas nucleares
| Coordenada interna |
|
| |
|
| R(OH) |
0.958 Å |
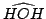 |
104.5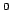 |
Solución:
Las distancias internucleares en este caso valen:
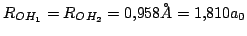
Como
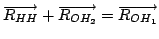 , tenemos que la
otra distancia
, tenemos que la
otra distancia 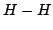 vale:
vale:
es decir,
y
- 63
- El primer estado excitado del
 se obtiene excitando un
electrón del OM antienlazante
se obtiene excitando un
electrón del OM antienlazante 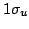 al OM enlazante
al OM enlazante 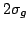 .
Escribe la configuración electrónica. ¿Cuales son las posibles
funciones de onda incluyendo el espín? ¿Cual es el orden de enlace?
Indicar si los estados electrónicos son
.
Escribe la configuración electrónica. ¿Cuales son las posibles
funciones de onda incluyendo el espín? ¿Cual es el orden de enlace?
Indicar si los estados electrónicos son 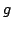 o
o 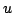 .
.
Solución:
La configuración electrónica del estado fundamental del He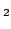 es:
es:
y la excitada
y las funciones de onda son, para el estado fundamental
y para los excitados
- 64
- Describir el estado electrónico fundamental y la multiplicidad,
utilizando las configuraciones electrónicas, de las siguientes
especies:
a) 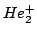 ,
b)
,
b) 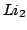 ,
c)
,
c) 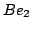 ,
d)
,
d) 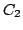 ,
e)
,
e) 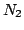 ,
f)
,
f) 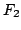 .
.
Solución:
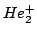 :
3 electrones
:
3 electrones
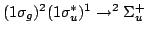
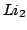 :
6 electrones
:
6 electrones
![$ [He_2] (2\sigma_g)^2 \rightarrow ^1\Sigma_g^+ $](img39.gif)
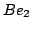 :
8 electrones
:
8 electrones
![$ [He_2] (2\sigma_g)^2 (2\sigma_u^*)^2 \rightarrow ^1\Sigma_g^+ $](img40.gif)
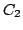 :
12 electrones
:
12 electrones
![$ [Be_2] (1\pi_u)^4 \rightarrow ^1\Sigma_g^+ $](img41.gif)
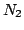 :
14 electrones
:
14 electrones
![$ [Be_2] (1\pi_u)^4 (3\sigma_g)^2 \rightarrow ^1\Sigma_g^+ $](img42.gif)
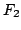 :
18 electrones
:
18 electrones
![$ [N_2] (1\pi_g^*)^4 \rightarrow ^1\Sigma_g^+ $](img43.gif)
- 65
- Calcular la densidad de probabilidad electrónica en el punto
medio de los hidrógenos en el
 para los estados descritos por
para los estados descritos por
a)
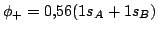 ,
b)
,
b)
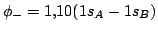
para la distancia internuclear 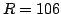 pm.
pm.
Solución:
Para ello necesitamos la expresión del orbital atómico
a)En este caso
y como en el centro 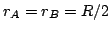 ,
,
Como en el equilibrio
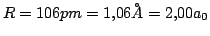 ,
,
que se puede comparar con el resultado
de considerar los átomos por separado:
luego
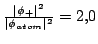 y la diferencia entre las densidades es
y la diferencia entre las densidades es
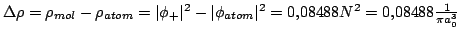
b)Análogamente
- 66
- Aplicando la teoría de orbitales moleculares, indíquese cuál de
las siguientes moléculas,
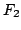 ,
, 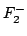 y
y 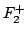 , tendrá
mayor energía de disociación.
, tendrá
mayor energía de disociación.
Solución:
Para saber cual de las moléculas tendría mayor enrgía de disociación necesitamos
calcular el orden de enlace:
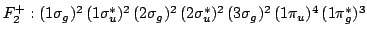 O.E.
O.E. 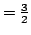
 O.E.
O.E. 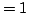 .
.
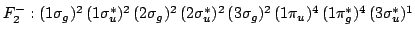 O.E.
O.E. 
El orden de energía de disociación es:
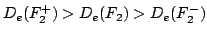
- 67
- Dibujar el diagrama de niveles de energía de la molécula de
 .
Determinar su estructura electrónica y justificar que su estado
fundamental es
.
Determinar su estructura electrónica y justificar que su estado
fundamental es 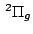 .
.
Solución:
La estructura electrónica del  es:
es:
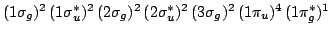
Para esta configuración el estado fundamental corresponde a 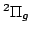
- 68
- Deducir el término espectral más estable correspondiente a
cada una de las siguientes configuraciones electrónicas de
moléculas
diatómicas homonucleares:
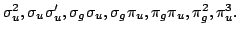
Solución:
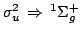
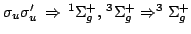
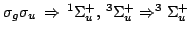
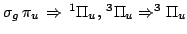
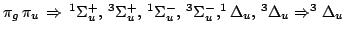
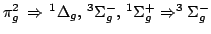
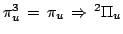
- 69
- Dadas las curvas de energía potencial para las moléculas
diatómicas
 y
y  , calcular la energía de disociación del
, calcular la energía de disociación del
 (
(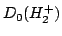 ) sabiendo que la energía de disociación del
) sabiendo que la energía de disociación del  es
es
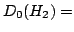 4.478 eV y que el potencial de ionización del
4.478 eV y que el potencial de ionización del  es
es
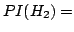 15.426 eV.
15.426 eV.
![\includegraphics[angle=0,scale=0.5]{fqcfig1.ps}](H2.gif)
Solución:
De la figura se deduce que:
Como
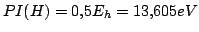 , tenemos
, tenemos
- 70
- Calcular
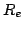 ,
, 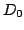 ,
, 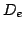 para las moléculas diatómicas
para las moléculas diatómicas  y
y
 de la gráfica anterior, así como el PI del
de la gráfica anterior, así como el PI del  .
.
- 71
- En la siguiente figura se representa la superficie de energía
potencial para la reacción colineal
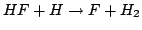 .
Indicar cuáles son los reactivos, productos, estado de transición y
dibujar cualitativamente el camino de mínima energía.
.
Indicar cuáles son los reactivos, productos, estado de transición y
dibujar cualitativamente el camino de mínima energía.
![\includegraphics[angle=0,scale=0.5]{fqcfig2.ps}](FH2.gif)
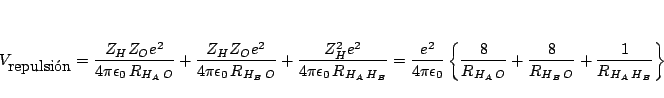
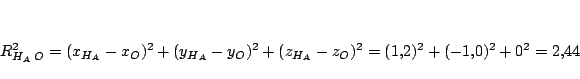
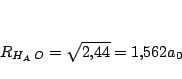
![]() y
y
![]() , por lo que
, por lo que
![]()
![]()
![]() , tenemos que la
otra distancia
, tenemos que la
otra distancia ![]() vale:
vale:

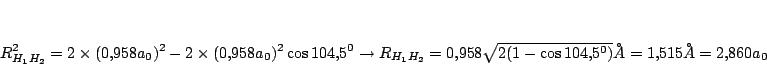
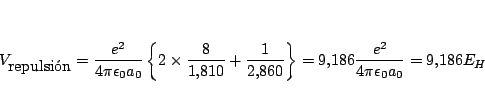
![]() es:
es:

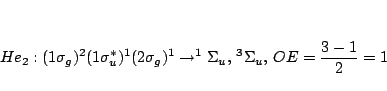
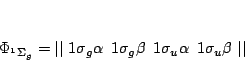
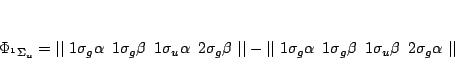

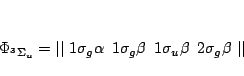
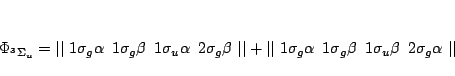
![]() ,
b)
,
b) ![]() ,
c)
,
c) ![]() ,
d)
,
d) ![]() ,
e)
,
e) ![]() ,
f)
,
f) ![]() .
.
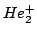 :
3 electrones
:
3 electrones
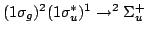
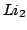 :
6 electrones
:
6 electrones
![$ [He_2] (2\sigma_g)^2 \rightarrow ^1\Sigma_g^+ $](img39.gif)
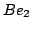 :
8 electrones
:
8 electrones
![$ [He_2] (2\sigma_g)^2 (2\sigma_u^*)^2 \rightarrow ^1\Sigma_g^+ $](img40.gif)
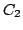 :
12 electrones
:
12 electrones
![$ [Be_2] (1\pi_u)^4 \rightarrow ^1\Sigma_g^+ $](img41.gif)
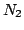 :
14 electrones
:
14 electrones
![$ [Be_2] (1\pi_u)^4 (3\sigma_g)^2 \rightarrow ^1\Sigma_g^+ $](img42.gif)
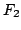 :
18 electrones
:
18 electrones
![$ [N_2] (1\pi_g^*)^4 \rightarrow ^1\Sigma_g^+ $](img43.gif)
![]() ,
b)
,
b)
![]()
![]() pm.
pm.
![\begin{displaymath}
1s= N \exp(-r/a_0) =
\left[\frac{1}{\pi a_0^3}\right]^{1/2} \exp(-r/a_0)
\end{displaymath}](img48.gif)
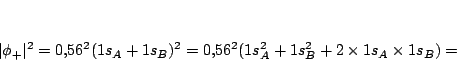
![\begin{displaymath}
0.56^2 N^2
\left[
\exp(-2 r_A/a_0) +
\exp(-2 r_B/a_0) +
2 \times \exp[- (r_A+r_B)/a_0]
\right]
\end{displaymath}](img50.gif)
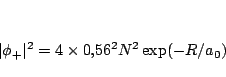
![]() ,
,
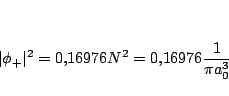
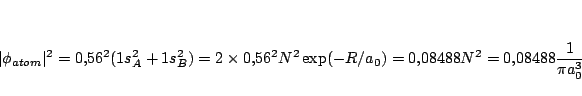
![\begin{displaymath}
\vert\phi_-\vert^2 = 0.56^2 (1s_A - 1s_B)^2=
0.56^2 (1s_A^2...
...\times 1s_A \times 1s_B) =
0 \left[\frac{1}{\pi a_0^3}\right]
\end{displaymath}](img58.gif)
![]() O.E.
O.E. ![]()
![]() O.E.
O.E. ![]() .
.
![]() O.E.
O.E. ![]()
![]()
![]() es:
es:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![\includegraphics[angle=0,scale=0.5]{fqcfig1.ps}](H2.gif)
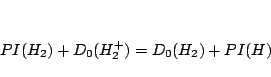
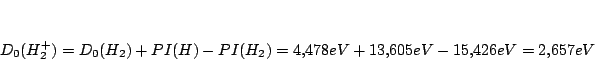
![\includegraphics[angle=0,scale=0.5]{fqcfig2.ps}](FH2.gif)