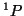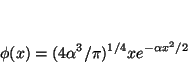
- Comprobar si existe algún valor de
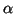 para el cual esta
función es solución de la ecuación de
Schrödinger para un oscilador armónico monodimensional de masa
para el cual esta
función es solución de la ecuación de
Schrödinger para un oscilador armónico monodimensional de masa 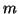 y
constante de fuerza
y
constante de fuerza 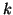 .
.
- Obtener la densidad de probabilidad en
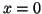 .
.
- Calcular las posiciones de los máximos de la densidad de probabilidad
en función de
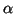 .
.
Solución:
- La ecuación de Schrödinger independiente del tiempo para el
oscilador armónico monodimensional es
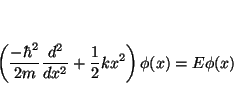
Para comprobar que es solución tenemos que sustituir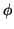 , para lo que necesitamos la segunda derivada
, para lo que necesitamos la segunda derivada
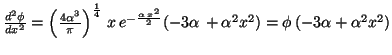
que será solución si:
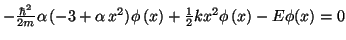
O lo que es lo mismo:
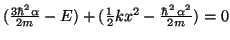
que será nulo para todo valor de
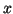 si:
si:
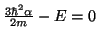
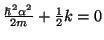
De la segunda ecuación obtenemos el valor de
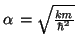
De la primera obetenemos el valor de la energía,
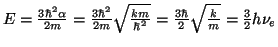
- La densidad de probabilidad para
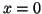 es:
es:
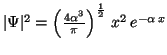 Para
Para
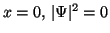 .
.
- Para calcular los máximos de la densidad, derivamos e igualamos a cero :
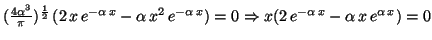
Los puntos críticos son:
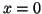 (mínimo).
(mínimo).
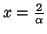 (máximo).
(máximo).
Solución:
Aplicando el método de separación de variables, obtenemos que los
niveles de energía se pueden expresar como
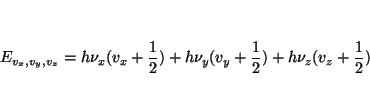
donde
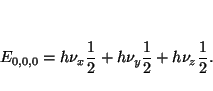
Solución:
La relación entre las coordenadas cartesianas y las polares es:
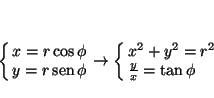
por lo que las derivadas se pueden calcular aplicando la regla de la cadena
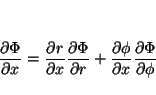
donde
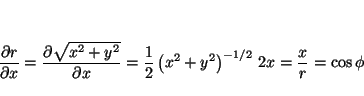
análogamente
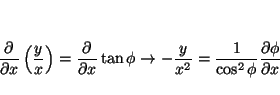
de donde se obtiene
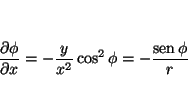
que permite calcular
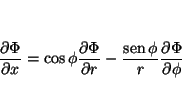
y
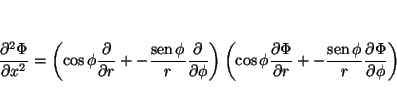
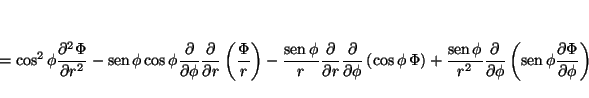
Análogamente
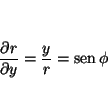
y
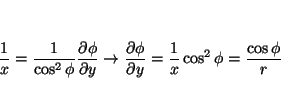
de donde se obtiene
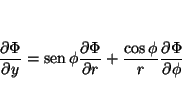
y
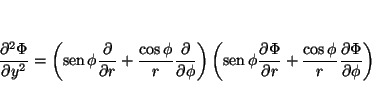
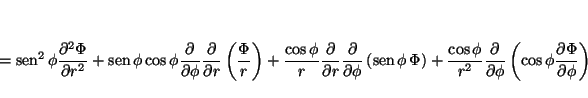
de tal forma que
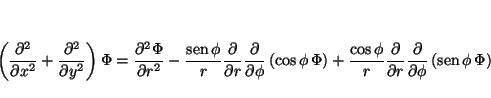
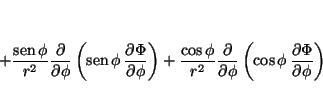
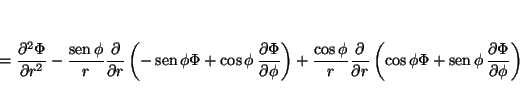
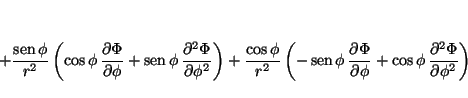
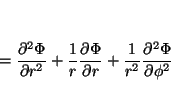
Solución:
La normalización se obtiene cuando
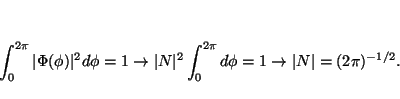
Solución:
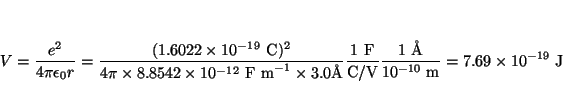
o en ergios
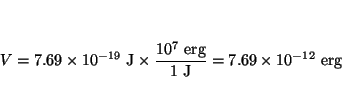
y en eV
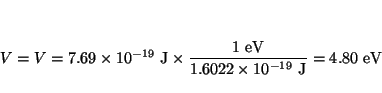
Solución:
La atracción gravitatoria es
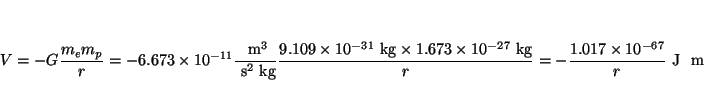
y la electrostática
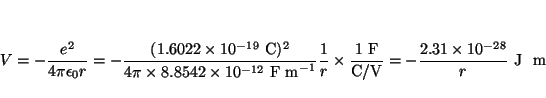
b) Verifique que para la función
![]() el requisito
el requisito
![]() conduce a la
condición de que
conduce a la
condición de que ![]() sea un número entero.
sea un número entero.
Solución:
a)
![]()
b)
![]()
![]()
Solución:
Como
![]() , tenemos que
, tenemos que
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
Solución:
![]()
luego
![]()
|
|
|
| 6561 | |
| 1640 | |
| 729 | |
| 410 |
La transición es posible para los estados que cumplen
![]() , luego son
, luego son
![]() ,
,
![]() y
y
![]() .
.
Solución:
![]() kg
y
kg
y
![]() kg,
luego
kg,
luego
![]()
![]() kg, luego
kg, luego
![]() , y
, y
![]()
y las energías de los niveles son (ya que ![]() )
)
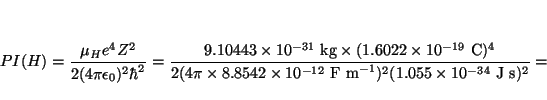
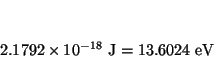
y
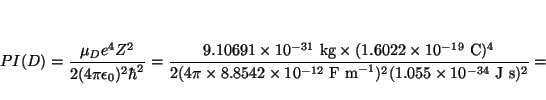
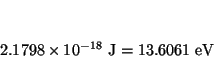
Las líneas de la serie de Balmer corresponden a la transición
![]() . La primera línea está a:
. La primera línea está a:
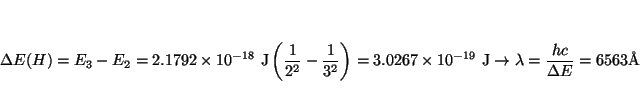
y
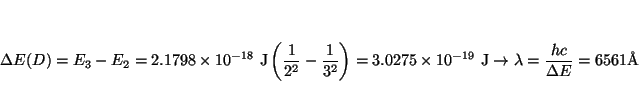
Solución:
Los números de onda de las transiciones son
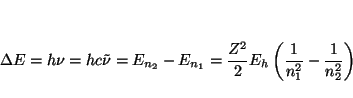
De la longitud de onda de las dos primeras líneas de la serie podemos
obtener el valor de ![]() y
y ![]() , ya que para la primera línea
, ya que para la primera línea
![]() y para la segunda
y para la segunda ![]()
![\begin{displaymath}
h c \tilde{\nu_1} =
\frac{Z^2}{2} E_h \left[ \frac{1}{n_1^2} - \frac{1}{(n_1+1)^2} \right]
\end{displaymath}](img110.gif)
y
![\begin{displaymath}
h c \tilde{\nu_2} =
\frac{Z^2}{2} E_h \left[ \frac{1}{n_1^2} - \frac{1}{(n_1+2)^2} \right]
\end{displaymath}](img111.gif)
y su cociente vale
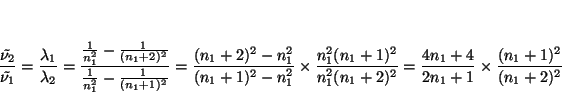
luego
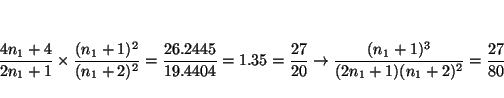
y como los dos miembros son números fraccionarios, los numeradores y denominadores son múltiplos entre si. En este caso (
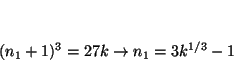
La primera posibilidad es
El valor de ![]() se obtiene de una de las líneas:
se obtiene de una de las líneas:
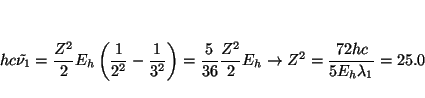
luego
(a)
![]() (b)
(b)
![]() (c)
(c)
![]() (d)
(d)
![]()
Solución:
Estarán permitidas aquellas en las que
![]() , es decir,
(b) y (d). Nótese sin embargo que la última transición no da
lugar a emisión o absorción de un fotón.
, es decir,
(b) y (d). Nótese sin embargo que la última transición no da
lugar a emisión o absorción de un fotón.
Solución:
La densidad de probabilidad radial se define como
![]() , donde
, donde ![]() es la parte radial de la función de onda del estado
fundamental. El máximo de la función de distribución radial se
obtiene igualando a cero la primera derivada
es la parte radial de la función de onda del estado
fundamental. El máximo de la función de distribución radial se
obtiene igualando a cero la primera derivada
![\begin{displaymath}
\left.
\frac{d P(r)}{d r}
\right\vert _{r_m}= 0
\rightarrow...
... \exp[-2Zr/a_0]
\right\vert _{r_m}= 0
\rightarrow r_m = a_0/Z
\end{displaymath}](img130.gif)
Luego para el C
Solución:
La función de onda del estado fundamental para un átomo hidrogenoide
es
![$\phi_{1s}= \left[\frac{Z^3}{\pi a_0^3}\right]^{1/2} \exp[-Zr/a_0]$](img133.gif) ,
por lo que
la probabilidad de encontrar el electrón en una esfera de radio
,
por lo que
la probabilidad de encontrar el electrón en una esfera de radio ![]() es
es
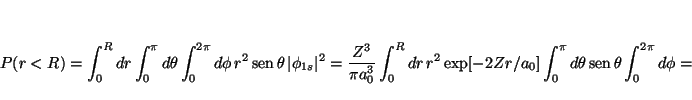
![\begin{displaymath}
\frac{Z^3}{\pi a_0^3} \int_0^R dr \, r^2 \exp[- 2 Zr/a_0]
\l...
...2 \pi =
\frac{4Z^3}{a_0^3} \int_0^R dr \, r^2 \exp[- 2 Zr/a_0]
\end{displaymath}](img136.gif)
que requiere del cálculo, por partes, de la siguiente integral
![\begin{displaymath}
I(R) = \int_0^R dr \, r^2 \exp[- \alpha r]
\end{displaymath}](img137.gif)
con
![\begin{displaymath}
I(R) = \frac{2}{\alpha^3}
\left[ 1 -
\left( \frac{\alpha^2 R^2}{2} + \alpha R + 1 \right)
\exp[ - \alpha R ]
\right]
\end{displaymath}](img139.gif)
y
![\begin{displaymath}
P(r<R) =
\frac{4 Z^3}{a_0^3}
\frac{2a_0^3}{8Z^3}
\left[ 1 -...
...0^2} + \frac{2ZR}{a_0} + 1 \right)
\exp[ - 2ZR/a_0 ]
\right]
=
\end{displaymath}](img140.gif)
![\begin{displaymath}
1 -
\left( \frac{2 Z^2 R^2}{a_0^2} + \frac{2ZR}{a_0} + 1 \right)
\exp[ - 2ZR/a_0 ]
\end{displaymath}](img141.gif)
| 1. | 0.72777 |
| 1.5 | 0.92153 |
| 2. | 0.98064 |
| 2.5 | 0.99566 |
| 3. | 0.99909 |
| 3.5 | 0.99982 |
| 4. | 0.99996 |
| 4.5 | 0.99999 |
| 1.00000 |
![$N= \left[\frac{Z^3}{\pi
a_0^3}\right]^{1/2}$](img145.gif)
Solución:
La condición de normalización es
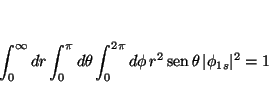
es decir, para el estado fundamental
![\begin{displaymath}
\vert N\vert^2 \int_0^\infty dr \, r^2 \exp[- 2 Zr/a_0]
\int...
... \exp[- 2 Zr/a_0]
\left[ - \cos \theta \right]_0^\pi 2 \pi = 1
\end{displaymath}](img147.gif)
![\begin{displaymath}
\vert N\vert^2 \int_0^\infty dr \, r^2 \exp[- 2 Zr/a_0]
4 \pi = 1
\end{displaymath}](img148.gif)
La integral en
![\begin{displaymath}
I(\infty) = \int_0^\infty dr \, r^2 \exp[- \alpha r] =
\frac{2}{\alpha^3}
\end{displaymath}](img150.gif)
con
![\begin{displaymath}
\vert N\vert^2 \frac{2a_0^3}{(2Z)^3}
4\pi = 1
\rightarrow
\vert N\vert = \left[\frac{Z^3}{\pi a_0^3}\right]^{1/2}
\end{displaymath}](img151.gif)
- Determinar el valor medio de la distancia del núcleo al
electrón para el orbital 1s del átomo de H y del ion He
 .
.
- Comparar los resultados del apartado anterior con el valor del máximo de la función de distribución radial.
- Determinar el valor medio de la energía potencial en ambos sistemas.
Solución:
-
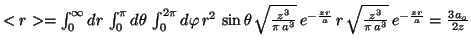
Para el hidrógeno,
 ,
,
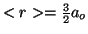 ,
para el He
,
para el He
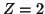 ,
,
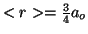
- La función de distribución radial es proporcional a
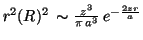
Para calcular el máximo se deriva la función y se iguala a cero:
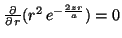 Se obtiene
Se obtiene
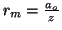 . Para el hidrógeno (
. Para el hidrógeno (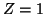 ),
), 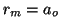 .
Para el He
.
Para el He
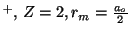
-
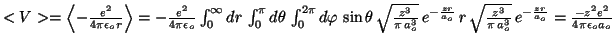
Para el hidrógeno
 , y
, y
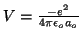 .
Para el He
.
Para el He y
y
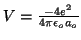
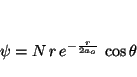
- Encontrar sus números cuánticos y decir de que orbital se trata.
- Usando los resultados del apartado anterior, decir cuánto vale el módulo del momento angular del electrón cuando está en este estado.
- Decir cuánto vale la proyección sobre el eje z del momento angular del electrón cuando está en este estado.
- Encontrar sus planos nodales.
- Comprobar que su constante de normalización vale
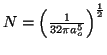
- Calcular el valor más probable de la distancia entre el electrón y el núcleo.
- Calcular la probabilidad de hallar el electrón entre los
valores de
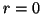 y
y 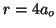 .
.
- Calcular el valor medio de
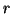 y de la energía potencial.
y de la energía potencial.
- Calcular la probabilidad de hallar el electrón
entre los valores de
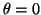 y
y
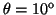 .
.
- Calcular la probabilidad de hallar el electrón
entre los valores de
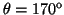 y
y
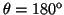 .
.
- Calcular la probabilidad de hallar el electrón
entre los valores de
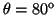 y
y
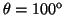 .
.
- Evaluar la densidad de probabilidad en los
puntos
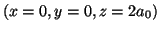 y
y
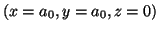 .
.
- Los números cuánticos son:
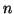 =2,
=2, 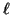 =1,
=1, 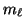 =0.
El orbital es: 2
=0.
El orbital es: 2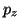 .
.
- El módulo del momento angular es :
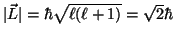 .
.
- La proyección del momento angular sobre el eje z es:
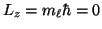 .
.
- Los planos nodales son:
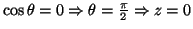 .
.
-
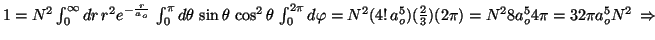
 .
.
- El valor de la distancia más probable es:
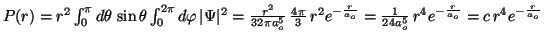 .
.
Derivamos la función P(r) para calcular los valores máximo y mínimo:
![$P^\prime(r) = c \, [4r^3 \, e^{-\frac{r}{a_o}}-\frac{1}{a_o} r^4 \, e^{-\frac{r}{a_o}}]=0$](img188.gif) .
.
Resolviendo esta ecuación obtenemos:
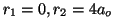 . El mínimo es
. El mínimo es 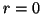 , y el
valor más probable es
, y el
valor más probable es 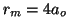 .
.
- La probabilidad es:
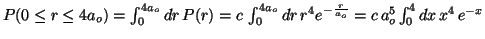 .
.
Resolviendo la integral por partes tomando u=
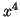 y v=
y v=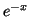 ,
el resultado es 0.371
,
el resultado es 0.371  37.1%.
37.1%.
- El valor del radio medio es:
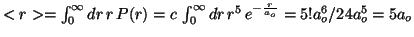 .
.
La energía potencial es:
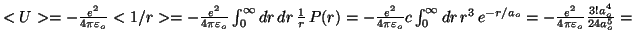
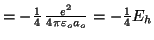 .
.
- La probabilidad entre
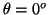 y
y 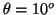 es:
es:
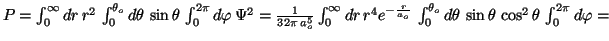
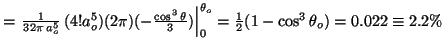 .
.
- La probabilidad entre
 y
y  es:
es:
![$P=\frac{1}{2} [\cos^3(170^o)-\cos^3(180^o)]=\frac{1}{2}[1+\cos^3(170^o)]=0.022$](img204.gif) .
.
- La probabilidad entre
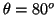 y
y 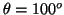 es:
es:
![$P=\frac{1}{2} [\cos^3(80^o)-\cos^3(100^o)]=0.005\equiv0.5\%$](img207.gif) .
.
- Para
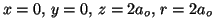 , la densidad de probabilidad es:
, la densidad de probabilidad es:
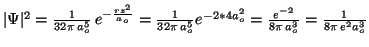 .
.
Para
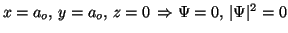 .
.
Solución:
La función ![]() será solución de la ecuación de Schrödinger
si cumple
será solución de la ecuación de Schrödinger
si cumple
![]() , donde el Hamiltoniano viene dado, en
coordenadas esféricas, por
, donde el Hamiltoniano viene dado, en
coordenadas esféricas, por
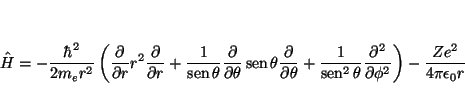
Veamos la aplicación de cada uno de los términos a la función
![\begin{displaymath}
\frac{\partial}{\partial r}
r^2
\frac{\partial}{\partial r}
...
...0} + \frac{Z^2r^2}{4a_0^2} \right)
r\exp[-Zr/2a_0]\cos\theta
=
\end{displaymath}](img215.gif)
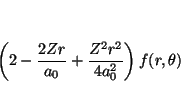
y
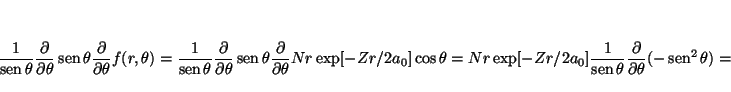
![\begin{displaymath}
N r \exp[-Zr/2a_0]
\frac{1}{\mathop{\rm sen}\nolimits \thet...
...s \theta)
=
-2 N r \exp[-Zr/2a_0] \cos \theta
=
-2 f(r,\theta)
\end{displaymath}](img218.gif)
y
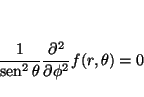
Así, obtenemos que
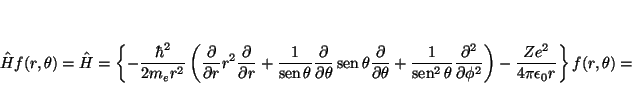
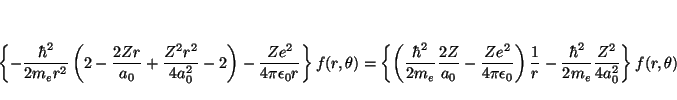
y como
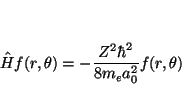
de donde se deduce que el valor de la energía es
(a) ![]() (b)
(b) ![]() (c)
(c)
![]() (d)
(d)
![]() (e)
(e)
![]()
donde ![]() y
y ![]() son funciones arbitrarias de las coordenadas de las
partículas idénticas 1 y 2,
son funciones arbitrarias de las coordenadas de las
partículas idénticas 1 y 2, ![]() ,
, ![]() son las distancias de las
partículas al núcleo y
son las distancias de las
partículas al núcleo y ![]() la distancia entre las dos.
la distancia entre las dos.
Solución:
Para saber si son o no antisimétricas con respecto al intercambio de las dos partículas idénticas, tenemos que intercambiarlas
(a)
![]() , luego ni es simétrica ni
antisimétrica (si
, luego ni es simétrica ni
antisimétrica (si ![]() y
y ![]() son distintas).
son distintas).
(b)
![]() , luego es simétrica.
, luego es simétrica.
(c)
![]() , luego es antisimétrica.
, luego es antisimétrica.
(d)
![]() , luego es simétrica.
, luego es simétrica.
(e)
![]() , luego es
antisimétrica.
, luego es
antisimétrica.
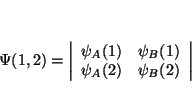
demostrar que
(a) el intercambio de 2 columnas cambia el signo de ![]() ,
,
(b) el intercambio de 2 filas cambia el signo de ![]() ,
,
(c) los dos electrones no pueden estar en el mismo espín-orbital.
Solución:
De la definición de determinante tenemos que
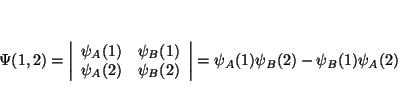
(a) Si intercambiamos 2 columnas, el determinante que queda es
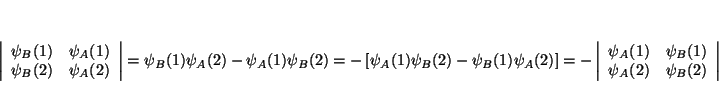
(b) si lo que intercambiamos son las 2 filas
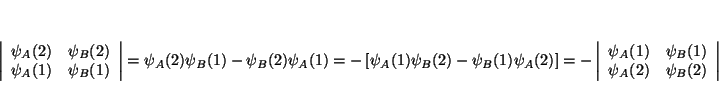
(c) Si dos electrones ocupan el mismo espín-orbital, entonces
![]() , y el determinante vale
, y el determinante vale
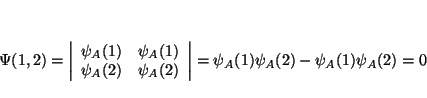
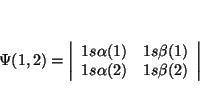
Solución:
De la definición de determinante tenemos que
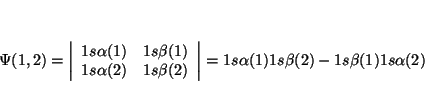
Si intercambiamos los dos electrones, el determinante queda
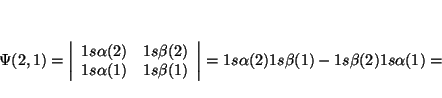
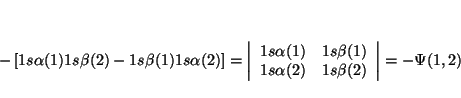
Solución:
La energía de los orbitales hidrogenoides es
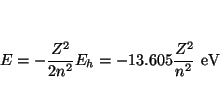
. Suponiendo valida una ecuación de este tipo (donde
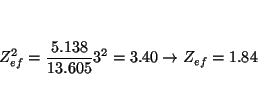
para el K
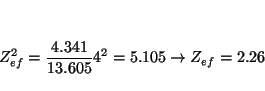
y para el Rb
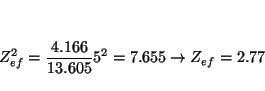
lo que indica que al bajar en un grupo la carga nuclear efectiva que siente el electrón de valencia es prácticamente constante (nótese que las cargas nucleares aumentan mucho:
Solución:
El Hamiltoniano para el átomo de Li es
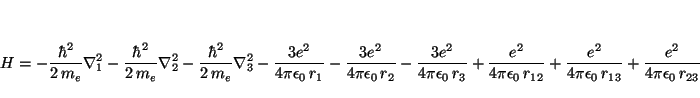
Solución:
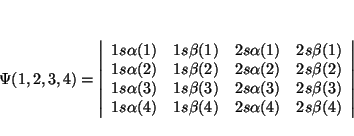
Solución:
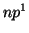
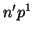 : En este caso
: En este caso 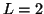 ,
, 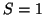 , es decir
, es decir
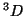
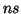
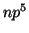 : Es análoga a
: Es análoga a 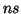
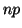 , luego es
, luego es
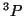
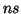
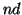 :
:
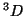
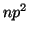 :
:
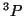
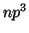 :
:
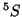
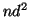 :
:
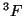
Solución:
- He(
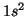 ):
):
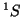
- Li(
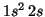 ):
):
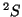
- Be(
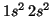 ):
):
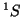
- B(
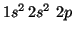 ):
):
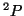
- C(
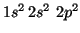 ):
):
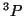
- N(
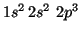 ):
):
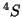
- O(
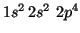 ):
):
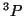
- F(
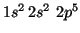 ):
):
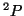
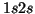 del átomo de He
del átomo de He
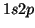 del átomo de He
del átomo de He
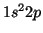 del átomo de Li
del átomo de Li
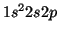 del átomo de Be
del átomo de Be
Solución:
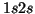 del átomo de He:
del átomo de He:
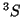 y
y 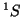
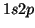 del átomo de He
del átomo de He
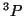 y
y 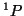
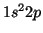 del átomo de Li
del átomo de Li
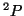
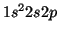 del átomo de Be
del átomo de Be
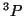 y
y