Solución:
(a)
![]() ,
,
(b)
![]() ,
,
(c)
![]() ,
,
(d)
![]() .
.
Solución:
Sea ![]() y
y ![]() con
con ![]() y
y ![]() reales, entonces
reales, entonces
![]() y
y
![]() .
.
Solución:
Si ![]() es solución de
es solución de
![]() ,
entonces
,
entonces ![]() también, ya que se cumple
también, ya que se cumple
![]() .
.
Solución:
Para una partícula libre la ecuación de Schrödinger monodimensional dependiente del tiempo es:
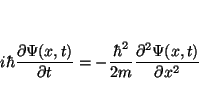
Para comprobar que es solución, calcularemos los dos miembros:
![\begin{displaymath}
i \hbar
\frac{\partial}{\partial t}
A \exp[2\pi i (\pm x/\...
...-\nu t)]=
A 2\pi \hbar \nu \exp[2\pi i (\pm x/\lambda -\nu t)]
\end{displaymath}](img30.gif)
y
![\begin{displaymath}
-\frac{\hbar^2}{2m}
\frac{\partial^2}{\partial x^2}
A \exp[...
...mbda^2} \frac{\hbar^2}{2m}
\exp[2\pi i (\pm x/\lambda -\nu t)]
\end{displaymath}](img31.gif)
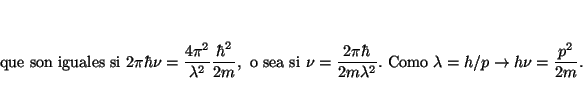
Solución:
De acuerdo con el principio de Incertidumbre
![]() , luego en este caso si
, luego en este caso si
![]() Å
Å
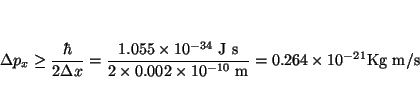
Si calculamos
![]() , vemos que en este
caso la indeterminación en la velocidad es del orden de la velocidad de
la luz.
, vemos que en este
caso la indeterminación en la velocidad es del orden de la velocidad de
la luz.
Solución:
De acuerdo con el principio de Incertidumbre
![]() , luego en este caso
, luego en este caso
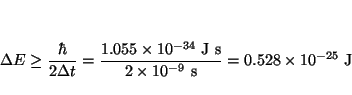
mientras que la energía con respecto al estado fundamental es de
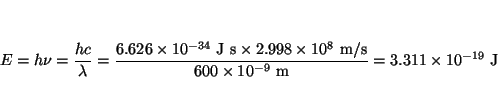
Solución:
Los niveles de energía de una caja monodimensional son:
![]() , que permite obtener la energía de la
transición
, que permite obtener la energía de la
transición
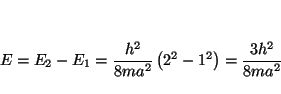
de donde se puede obtener la frecuencia de la luz emitida
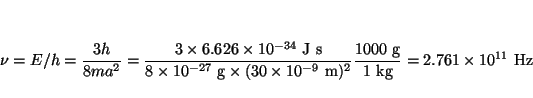
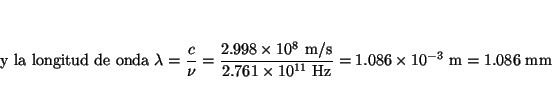
Solución:
Los niveles de energía de una caja monodimensional son:
![]() , que permite obtener la energía de los
niveles:
, que permite obtener la energía de los
niveles:
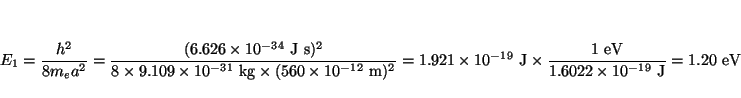
Si expresamos la energía del estado ![]() en función de la energía del
estado fundamental
en función de la energía del
estado fundamental
![]() :
:
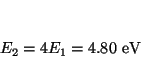
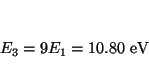
Solución:
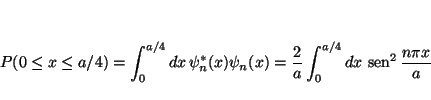
que se resuelve haciendo la sustitución
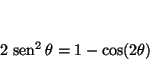
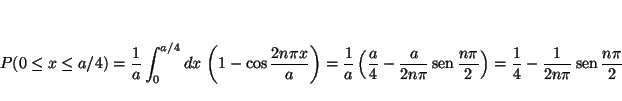
Nótese que si
Solución:
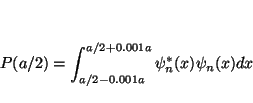
Como la función de onda casi no varía en dicho intervalo, se puede tomar como constante e igual al valor en
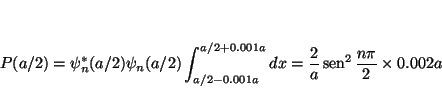
Para el estado fundamental ![]()
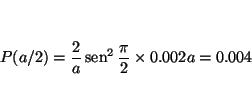
Solución:
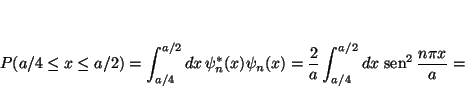
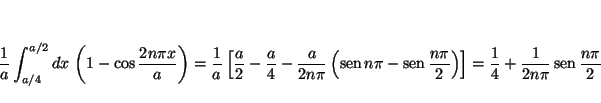
Solución:
En este caso
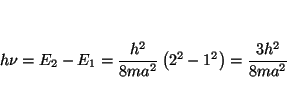
luego
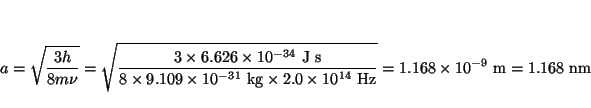
Solución:
La energía para una caja monodimensional de longitud ![]() es
es
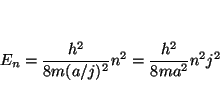
luego al dividir la longitud de la caja
Solución:
Para una partícula en una caja tridimensional de lados ![]() y
y ![]() , la
ecuación de Schrödinger independiente del tiempo es:
, la
ecuación de Schrödinger independiente del tiempo es:
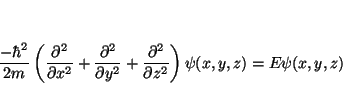
Aplicando el método de separación de variables, buscaremos soluciones de la forma
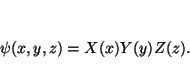
Sustituyendo en la ecuación y dividiendo por
![\begin{displaymath}
\frac{-\hbar^2}{2m}
\left[
\frac{1}{X(x)} \frac{d^2 X(x)}{d ...
...y)}{d y^2} +
\frac{1}{Z(z)} \frac{d^2 Z(z)}{d z^2}
\right] = E
\end{displaymath}](img90.gif)
De donde se deduce que cada uno de los términos del primer miembro tienen que ser constantes. Denominándolas
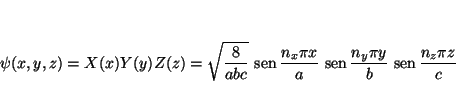
con
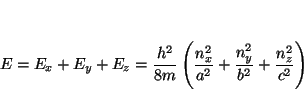
Solución:

de donde se deduce (a) que el número de estados con energías en el rango de 0 a
|
|
degeneración | |
| 1 1 1 | 3 | 1 |
| 1 1 2 | 6 | 3 |
| 1 2 1 | 6 | |
| 2 1 1 | 6 | |
| 1 2 2 | 9 | 3 |
| 2 1 2 | 9 | |
| 2 2 1 | 9 | |
| 1 1 3 | 11 | 3 |
| 1 3 1 | 11 | |
| 3 1 1 | 11 | |
| 2 2 2 | 12 | 1 |
| 1 2 3 | 14 | 6 |
| 1 3 2 | 14 | |
| 2 1 3 | 14 | |
| 2 3 1 | 14 | |
| 3 1 2 | 14 | |
| 3 2 1 | 14 |
Solución:
![\begin{displaymath}
\mbox{En este caso los niveles de energía son }
E_{n_x, n_y,...
...2}{8m a^2} \left[ n_x^2 + 2\left(n_y^2 + n_z^2 \right) \right]
\end{displaymath}](img103.gif)
En el rango de números cuánticos de 1 a 5 existen 125 estados, pondremos aquí solamente los 25 primeros
|
|
degeneración | |
| 1 1 1 | 5 | 1 |
| 2 1 1 | 8 | 1 |
| 1 1 2 | 11 | 2 |
| 1 2 1 | 11 | |
| 3 1 1 | 13 | 1 |
| 2 1 2 | 14 | 2 |
| 2 2 1 | 14 | |
| 1 2 2 | 17 | 1 |
| 3 1 2 | 19 | 2 |
| 3 2 1 | 19 | |
| 2 2 2 | 20 | 2 |
| 4 1 1 | 20 | |
| 1 1 3 | 21 | 2 |
| 1 3 1 | 21 | |
| 2 1 3 | 24 | 2 |
| 2 3 1 | 24 | |
| 3 2 2 | 25 | 1 |
| 4 1 2 | 26 | 2 |
| 4 2 1 | 26 | |
| 1 2 3 | 27 | 2 |
| 1 3 2 | 27 | |
| 3 1 3 | 29 | 3 |
| 3 3 1 | 29 | |
| 5 1 1 | 29 | |
| 2 2 3 | 30 | 2 |
| 2 3 2 | 30 |
Nótese que en este caso además de degeneración debida a la simetría
se producen casos de degeneración accidental (Véase cuando la energía
vale
![]() ).
).
Solución:
La ecuación de Schrödinger independiente del tiempo para el
oscilador armónico monodimensional es
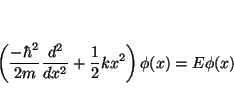
Para comprobar que es solución tenemos que sustituir
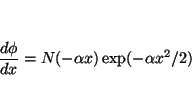
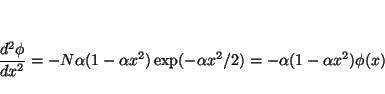
que será solución si
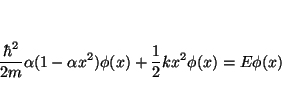
o lo que es lo mismo, si reordenamos
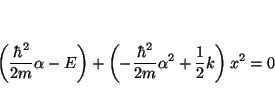
que será nulo para todo valor de
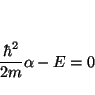
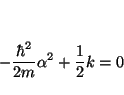
De la segunda ecuación obtenemos el valor de
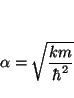
y de la primera el valor de la energía correspondiente a dicho estado
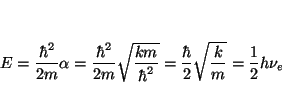
donde
Solución:
En este caso
![]() , donde
, donde ![]() es la masa reducida definida por
es la masa reducida definida por
![]() .
.
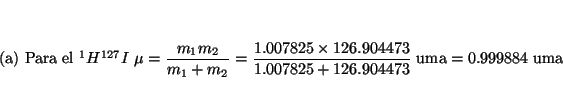
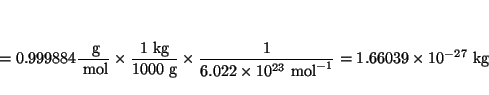
de donde se deduce que
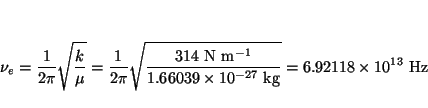
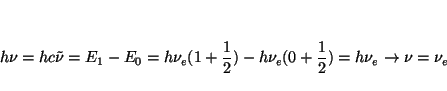
y (b)
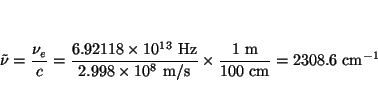
.
Análogamente para el ![]() :
:
![]() , y
(a)
, y
(a)
![]() y
(b)
y
(b)
![]() .
.
Solución:
Como
![]() , la frecuencia de la transición es
, la frecuencia de la transición es
![]() .
.