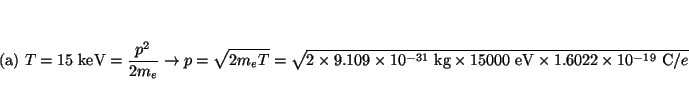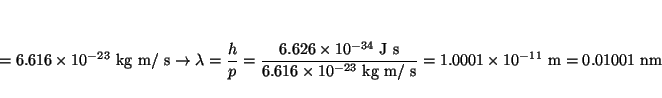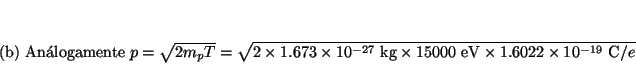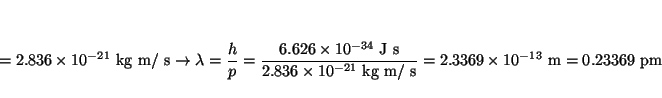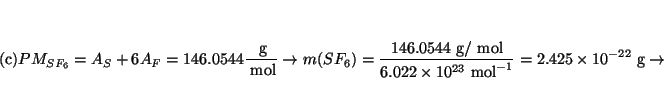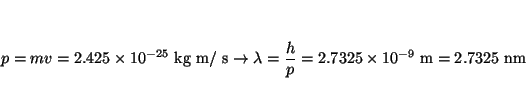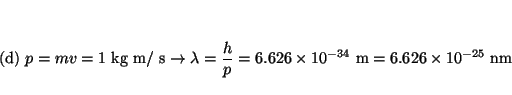- El oído humano es sensible a ondas sonoras con frecuencias
comprendidas entre 15 Hz y 20 kHz. La velocidad del sonido en el aire es
343 m/s. Calcular las longitudes de onda correspondientes a estas
frecuencias.
Solución:
- La línea más intensa del espectro del átomo de sodio tiene una
longitud de onda de 589 nm. Calcular el correspondiente número de
onda y la energía de la transición implicada en electronvoltios por
fotón, y en kJ/mol.
Solución:
- Calcular la longitud de onda máxima de un fotón que pueda producir
la reacción:
Solución:
que corresponde con la energía de un fotón capaz de producir la
reacción:
- La reacción fotoquímica
es una de las fuentes de átomos de oxígeno (y por tanto de ozono)
más importante en la atmósfera terrestre. La energía de disociación es
306 kJ/mol. Encontrar la longitud de onda de un fotón capaz de producir
dicha reacción.
Solución:
- La frecuencia umbral para la emisión fotoeléctrica del cobre es
1.1
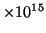 s
s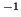 . ¿Cuál será la energía
máxima (en electronvoltios) de los fotoelectrones emitidos cuando la
luz de frecuencia 1.5
. ¿Cuál será la energía
máxima (en electronvoltios) de los fotoelectrones emitidos cuando la
luz de frecuencia 1.5
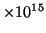 s
s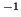 incide sobre una
superficie de cobre?.
incide sobre una
superficie de cobre?.
Solución:
De acuerdo con el principio de conservación de la energía
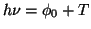 , donde
, donde 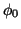 es la energía mínima
necesaria para arrancar un electrón y T su energía cinética máxima.
es la energía mínima
necesaria para arrancar un electrón y T su energía cinética máxima.
La frecuencia umbral es (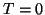 )
)
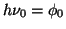 , que nos permite
reescribir la conservación de la energía:
, que nos permite
reescribir la conservación de la energía:
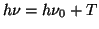 .
De donde
.
De donde
- El potencial de extracción del sodio es 2.3 eV:
a) ¿cuál será la máxima longitud de onda de la luz, que producirá
emisión de fotoelectrones en el sodio? y
b) ¿cuál será la energía
cinética máxima de los fotoelectrones si luz de 2000 Å
incide sobre una superficie de sodio?.
Solución:
y que corresponde con luz visible-ultravioleta.
- La función trabajo del K es 2.2 eV y la del Ni 5.0 eV.
(a) Calcular las frecuencias y longitudes de onda
umbral para estos dos metales. (b) ¿Dará lugar la luz ultravioleta de
longitud de onda 400 nm al efecto fotoeléctrico en el K? ¿Y en el Ni?
(c) Calcular la máxima energía cinética de los electrones emitidos en
(b).
Solución:
Análogamente, para el Níquel
(b) Si
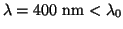 , si se dará el efecto
fotoeléctrico, mientras que si
, si se dará el efecto
fotoeléctrico, mientras que si
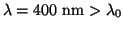 , no se
dará. Por tanto, en el K si y en el Ni no.
, no se
dará. Por tanto, en el K si y en el Ni no.
- Cuando se ilumina una cierta superficie metálica con luz de
diferentes longitudes de onda y se miden los potenciales que detienen los
fotoelectrones, se obtienen los valores que se muestran en la siguiente
tabla:
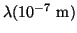 |
3.66 |
4.05 |
4.36 |
4.92 |
5.46 |
5.79 |
| V(V) |
1.48 |
1.15 |
0.93 |
0.62 |
0.36 |
0.24 |
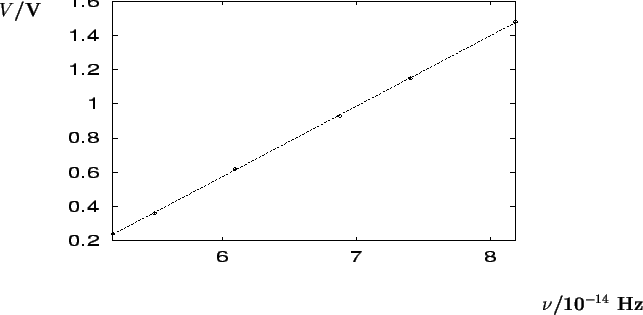
Representando el potencial en función de la frecuencia,
determinar: (a) la frecuencia umbral,
(b) el potencial de extracción del metal, y
(c) la constante de Planck.
Solución:
Representando el potencial en función de la frecuencia,
tenemos que:
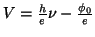
Si calculamos las frecuencias
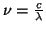
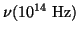 |
8.191 |
7.402 |
6.876 |
6.093 |
5.491 |
5.178 |
| V(V) |
1.48 |
1.15 |
0.93 |
0.62 |
0.36 |
0.24 |
Un ajuste por mínimos cuadrados da
de donde se deduce que
que permite determinar 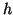 con un error del
con un error del
(c) Análogamente
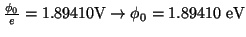 .
.
- Cuando cierto metal se irradia con luz de frecuencia
3.0
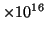 s
s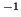 , los fotoelectrones emitidos
tienen una energía cinética doce veces mayor que los fotoelectrones
emitidos cuando el mismo metal se irradia con luz de frecuencia
2.0
, los fotoelectrones emitidos
tienen una energía cinética doce veces mayor que los fotoelectrones
emitidos cuando el mismo metal se irradia con luz de frecuencia
2.0
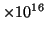 s
s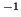 ¿Cuál será la frecuencia
umbral del metal?.
¿Cuál será la frecuencia
umbral del metal?.
Solución:
Como
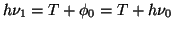 , tenemos un sistema de dos
ecuaciones con dos incógnitas
, tenemos un sistema de dos
ecuaciones con dos incógnitas
por lo que restándolas
- En un tubo de rayos X donde los electrones se aceleran con un
potencial de 5000 V, la mínima longitud de onda de los rayos X
producidos es 248 pm. Estimad el valor de la constante de Planck.
Solución:
En este caso la energía cinética de los electrones es igual a la
energía de los rayos X,
- Calcular la frecuencia hacia la cual convergen todas las líneas
espectrales de la serie de Lyman. ¿Cuál será la longitud de
onda y la energía de esta radiación?.
Solución:
El número de onda de las lineas de la serie de Lyman viene dada
por
con 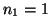 ,
,
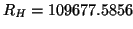 cm
cm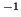 (constante de Rydberg para el
hidrógeno). La frecuencia a la cual convergen todas las lineas se
obtiene cuando
(constante de Rydberg para el
hidrógeno). La frecuencia a la cual convergen todas las lineas se
obtiene cuando 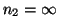 :
:
La frecuencia será
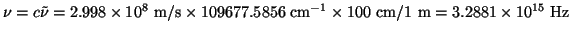 .
.
La longitud de onda es el inverso del número de onda
y la energía de la transición:
- Calcular la longitud de onda en Angstrom y la frecuencia en
s
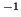 de la primera línea de la serie de Balmer.
de la primera línea de la serie de Balmer.
Solución:
con 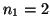 y
y 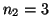 .
.
- Calcular el potencial de ionización del átomo de hidrógeno cuando
el electrón ocupa la órbita con número cuántico principal igual a 5.
Solución:
En este caso 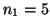 y
y 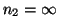 :
:
- Calcular la longitud de onda de De Broglie asociada a:
(a) un electrón con 15 keV de energía cinética,
(b) un protón con 15 keV de energía cinética,
(c) una molécula de SF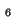 a una velocidad de
1 m/s, y
(d) un objeto de 1 kg a una velocidad de 1 m/s.
a una velocidad de
1 m/s, y
(d) un objeto de 1 kg a una velocidad de 1 m/s.
Solución:
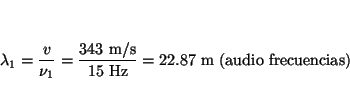
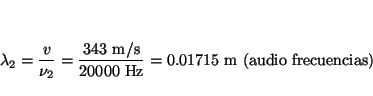
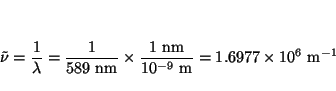
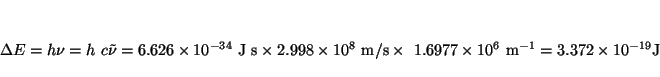
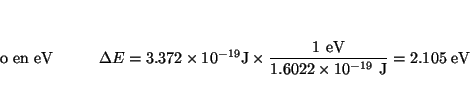
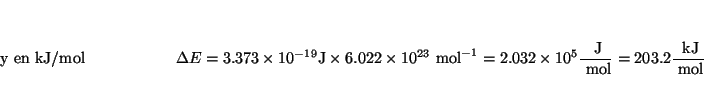
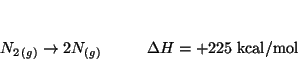
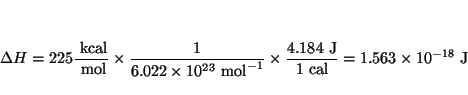
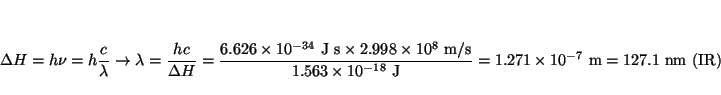
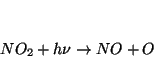
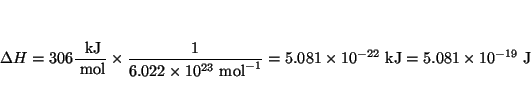
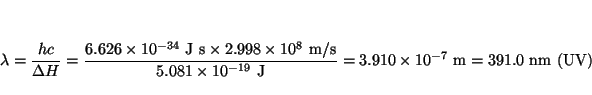
![]() , donde
, donde ![]() es la energía mínima
necesaria para arrancar un electrón y T su energía cinética máxima.
es la energía mínima
necesaria para arrancar un electrón y T su energía cinética máxima.
![]() )
)
![]() , que nos permite
reescribir la conservación de la energía:
, que nos permite
reescribir la conservación de la energía:
![]() .
De donde
.
De donde
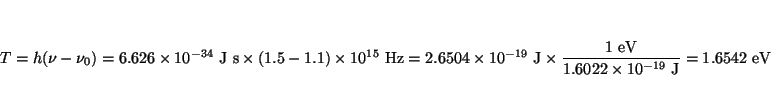
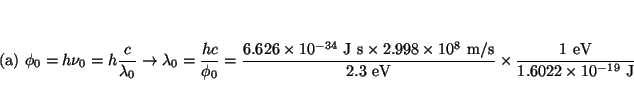
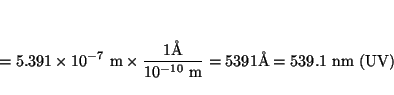
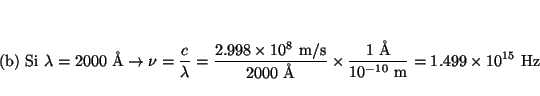
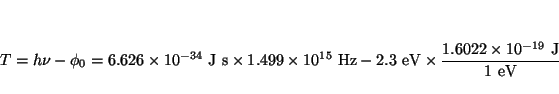
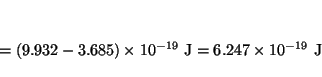
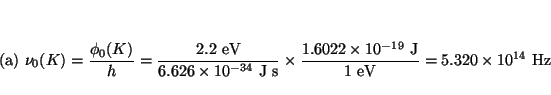
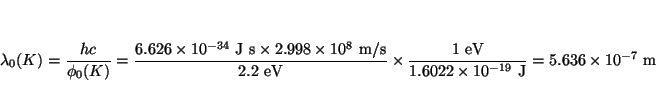
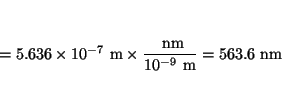
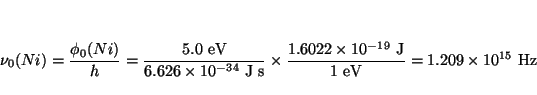
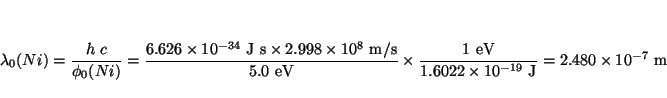
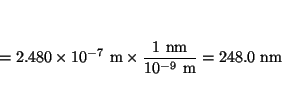
![]() , si se dará el efecto
fotoeléctrico, mientras que si
, si se dará el efecto
fotoeléctrico, mientras que si
![]() , no se
dará. Por tanto, en el K si y en el Ni no.
, no se
dará. Por tanto, en el K si y en el Ni no.
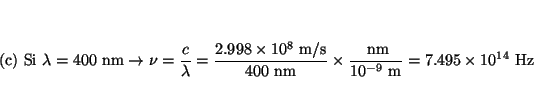
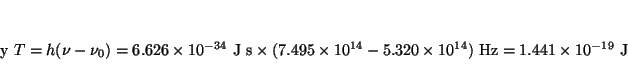
![]()
![]()
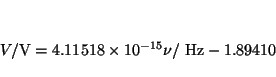
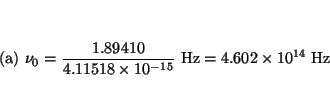
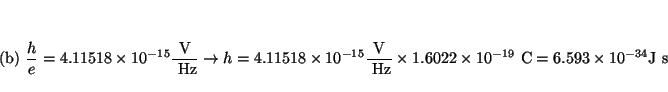
![]() con un error del
con un error del
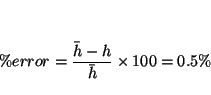
![]() .
.
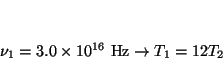
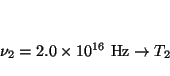
![]() , tenemos un sistema de dos
ecuaciones con dos incógnitas
, tenemos un sistema de dos
ecuaciones con dos incógnitas
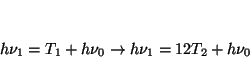
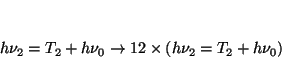
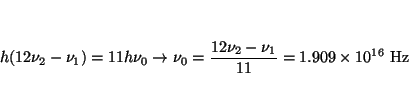
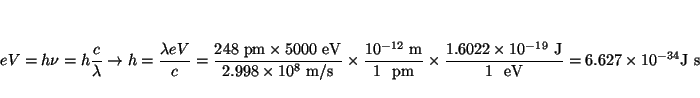
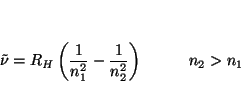
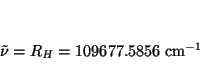
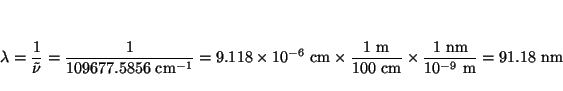
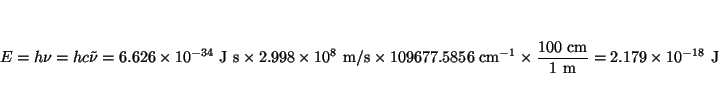
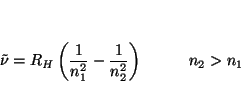
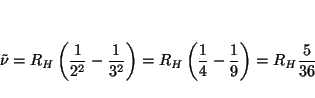
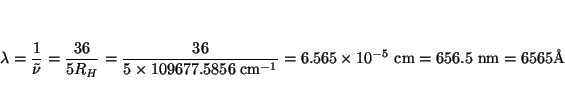
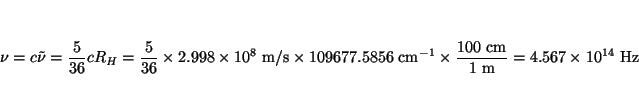
![]() y
y ![]() :
:
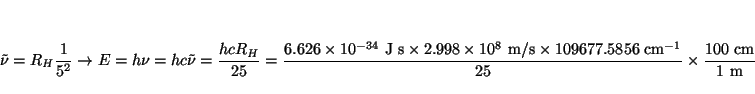
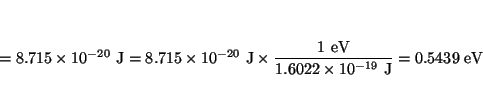
![]() a una velocidad de
1 m/s, y
(d) un objeto de 1 kg a una velocidad de 1 m/s.
a una velocidad de
1 m/s, y
(d) un objeto de 1 kg a una velocidad de 1 m/s.