- Comprobar si existe algún valor de
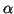 para el cual esta
función es solución de la ecuación de
Schrödinger para un oscilador armónico monodimensional de masa
para el cual esta
función es solución de la ecuación de
Schrödinger para un oscilador armónico monodimensional de masa  y
constante de fuerza
y
constante de fuerza 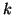 .
.
- Obtener la densidad de probabilidad en
 .
.
- Calcular las posiciones de los máximos de la densidad de probabilidad
en función de
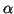 .
.
b) Verifique que para la función
![]() el requisito
el requisito
![]() conduce a la
condición de que
conduce a la
condición de que ![]() sea un número entero.
sea un número entero.
(a)
![]() (b)
(b)
![]() (c)
(c)
![]() (d)
(d)
![]()
- Determinar el valor medio de la distancia del núcleo al
electrón para el orbital 1s del átomo de H y del ion He
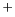 .
.
- Comparar los resultados del apartado anterior con el valor del máximo de la función de distribución radial.
- Determinar el valor medio de la energía potencial en ambos sistemas.
- Encontrar sus números cuánticos y decir de que orbital se trata.
- Usando los resultados del apartado anterior, decir cuánto vale el módulo del momento angular del electrón cuando está en este estado.
- Decir cuánto vale la proyección sobre el eje z del momento angular del electrón cuando está en este estado.
- Encontrar sus planos nodales.
- Comprobar que su constante de normalización vale
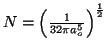
- Calcular el valor más probable de la distancia entre el electrón y el núcleo.
- Calcular la probabilidad de hallar el electrón entre los
valores de
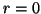 y
y 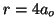 .
.
- Calcular el valor medio de
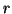 y de la energía potencial.
y de la energía potencial.
- Calcular la probabilidad de hallar el electrón
entre los valores de
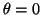 y
y
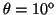 .
.
- Calcular la probabilidad de hallar el electrón
entre los valores de
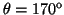 y
y
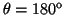 .
.
- Calcular la probabilidad de hallar el electrón
entre los valores de
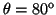 y
y
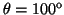 .
.
- Evaluar la densidad de probabilidad en los
puntos
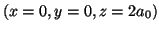 y
y
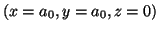 .
.
(a) ![]() (b)
(b) ![]() (c)
(c)
![]() (d)
(d)
![]() (e)
(e)
![]()
donde ![]() y
y ![]() son funciones arbitrarias de las coordenadas de las
partículas idénticas 1 y 2,
son funciones arbitrarias de las coordenadas de las
partículas idénticas 1 y 2, ![]() ,
, ![]() son las distancias de las
partículas al núcleo y
son las distancias de las
partículas al núcleo y ![]() la distancia entre las dos.
la distancia entre las dos.
demostrar que
(a) el intercambio de 2 columnas cambia el signo de ![]() ,
,
(b) el intercambio de 2 filas cambia el signo de ![]() ,
,
(c) los dos electrones no pueden estar en el mismo espín-orbital.
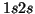 del átomo de He
del átomo de He
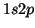 del átomo de He
del átomo de He
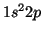 del átomo de Li
del átomo de Li
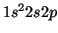 del átomo de Be
del átomo de Be