Fundamentos de Química Cuántica - Problemas (2006/07) Tema 2
- 15
- Calcular el módulo de (a)
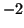 , (b)
, (b) 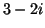 , (c)
, (c)
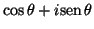 , (d)
, (d) 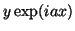 .
.
- 16
- Probar que
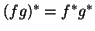 donde
donde 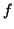 y
y 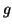 son cantidades
complejas.
son cantidades
complejas.
- 17
- Verificar que si
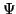 es una solución de la ecuación de
Schrödinger dependiente del tiempo, entonces
es una solución de la ecuación de
Schrödinger dependiente del tiempo, entonces 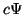 es también
solución siendo
es también
solución siendo 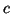 una constante.
una constante.
- 18
- Comprobar que las funciones
![$\Psi(x,t) = A \exp[2\pi i
(\pm x/\lambda -\nu t)]$](img13.gif) son soluciones de la ecuación de Schrödinger
monodimensional dependiente del tiempo
de una partícula libre. Suponiendo que
son soluciones de la ecuación de Schrödinger
monodimensional dependiente del tiempo
de una partícula libre. Suponiendo que 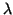 es la longitud de
onda de De Broglie, expresar
es la longitud de
onda de De Broglie, expresar 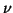 en función del momento lineal
en función del momento lineal 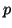 .
.
- 19
- Si la posición de un electrón se mide con una precisión de
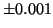 Å ¿Cuál será la máxima precisión para el momento?
Å ¿Cuál será la máxima precisión para el momento?
- 20
- Un átomo sufre una transición desde un estado excitado con un
tiempo de vida de 1 ns al estado fundamental, y emite un fotón con una
longitud de onda de 600 nm. Calcular la incertidumbre en la energía del
estado excitado.
- 21
- Hallar la longitud de onda de la luz emitida cuando una partícula
de
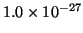 g en una caja monodimensional de 30 nm pasa del
nivel
g en una caja monodimensional de 30 nm pasa del
nivel 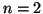 al nivel
al nivel 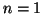 .
.
- 22
- Calcular la energía en electronvoltios (eV) de los niveles
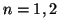 y 3 de un electrón en una caja de potencial monodimensional de
longitud
y 3 de un electrón en una caja de potencial monodimensional de
longitud 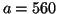 pm.
pm.
- 23
- Para una partícula en el estado estacionario
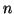 de una caja
monodimensional de longitud
de una caja
monodimensional de longitud 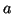 , encontrar la probabilidad de que la
partícula esté en la región
, encontrar la probabilidad de que la
partícula esté en la región
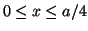 .
.
- 24
- Para el estado fundamental de una partícula en una caja
monodimensional de longitud
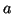 , encontrar la probabilidad de que la
partícula esté entre
, encontrar la probabilidad de que la
partícula esté entre 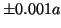 del punto
del punto 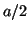 .
Calcular el valor medio de la posición y el momento.
.
Calcular el valor medio de la posición y el momento.
- 25
- Para el estado estacionario de número cuántico
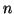 de la partícula
en una caja, escribir una expresión para la probabilidad de que la
partícula se encuentre entre
de la partícula
en una caja, escribir una expresión para la probabilidad de que la
partícula se encuentre entre 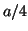 y
y 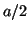 .
.
- 26
- Para un electrón en una determinada caja monodimensional, la
transición observada de menor frecuencia es
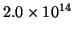 s
s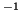 . Calcular la longitud de la caja.
. Calcular la longitud de la caja.
- 27
- Teniendo en cuenta las condiciones de continuidad que la función
de onda debe satisfacer, que pasaría a los niveles de energía de una
partícula en una caja monodimensional si la longitud de la caja cambia
de
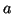 a
a 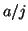 (
(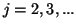 ).
).
- 28
- Encontrar las funciones de onda y las correspondientes energías
para los estados estacionarios de una partícula en una caja de potencial
tridimensional de lados
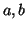 y
y 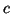 .
.
- 29
- Para una partícula en una caja cúbica de lado
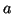 : (a) ¿Cuántos
estados tienen energías en el rango de 0 a
: (a) ¿Cuántos
estados tienen energías en el rango de 0 a 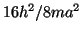 ? (b) ¿Cuántos
niveles de energía caen en ese rango?.
? (b) ¿Cuántos
niveles de energía caen en ese rango?.
- 30
- Para una partícula en una caja tridimensional de lados
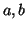 y
y
 con
con 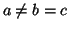 , hacer una tabla de
, hacer una tabla de 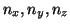 , las energías y
las degeneraciones de los niveles con números cuánticos en el rango de 1
a 5 (Tomar
, las energías y
las degeneraciones de los niveles con números cuánticos en el rango de 1
a 5 (Tomar 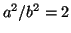 ).
).
- 31
- Comprobar que la función
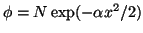 es
solución de la ecuación de Schrödinger para un oscilador armónico.
Relacionar
es
solución de la ecuación de Schrödinger para un oscilador armónico.
Relacionar 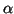 con la constante de fuerza del oscilador y la masa
de la partícula, y calcular la energía correspondiente a esa solución.
Calcular el valor medio de la posición de la partícula.
con la constante de fuerza del oscilador y la masa
de la partícula, y calcular la energía correspondiente a esa solución.
Calcular el valor medio de la posición de la partícula.
- 32
- La molécula
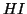 tiene una constante de fuerza de enlace de 314
Nm
tiene una constante de fuerza de enlace de 314
Nm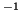 . Calcular para
. Calcular para 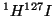 y
y 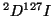 : (a) La frecuencia
vibracional clásica en s
: (a) La frecuencia
vibracional clásica en s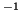 , (b) el número de onda correspondiente a
la transición de
, (b) el número de onda correspondiente a
la transición de 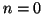 a
a 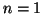 en el espectro vibracional.
en el espectro vibracional.
- 33
- Calcular la frecuencia de la radiación emitida cuando un
oscilador armónico de frecuencia 6.0
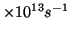 salta del
nivel
salta del
nivel 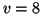 al
al 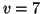 .
.
© Copyright.
Noemí Fernández
2003-03-26
![\begin{figure}\setlength{\unitlength}{1.cm}%%
\begin{picture}(10,5)(0,0)
\put(1....
...0){$a$}}
\put(12.3,4.5){\makebox(0,0)[l]{$\psi_3(x)$}}
\end{picture}\end{figure}](img23.gif)
![\begin{figure}\setlength{\unitlength}{1.cm}%%
\begin{picture}(10,5)(0,0)
\put(1....
...t(12.3,4.5){\makebox(0,0)[l]{$\vert\psi_3(x)\vert^2$}}
\end{picture}\end{figure}](img24.gif)
![\begin{figure}\setlength{\unitlength}{1.cm}%%
\begin{picture}(10,5)(0,0)
\put(1....
...0){$a$}}
\put(12.3,4.5){\makebox(0,0)[l]{$\psi_3(x)$}}
\end{picture}\end{figure}](img23.gif)
![\begin{figure}\setlength{\unitlength}{1.cm}%%
\begin{picture}(10,5)(0,0)
\put(1....
...t(12.3,4.5){\makebox(0,0)[l]{$\vert\psi_3(x)\vert^2$}}
\end{picture}\end{figure}](img24.gif)