- El oído humano es sensible a ondas sonoras con frecuencias
comprendidas entre 15 Hz y 20 kHz. La velocidad del sonido en el aire es
343 m/s. Calcular las longitudes de onda correspondientes a estas
frecuencias.
- La línea más intensa del espectro del átomo de sodio tiene una
longitud de onda de 589 nm. Calcular el correspondiente número de
onda y la energía de la transición implicada en electronvoltios por
fotón, y en kJ/mol.
- Calcular la longitud de onda máxima de un fotón que pueda producir
la reacción:
- La reacción fotoquímica
es una de las fuentes de átomos de oxígeno (y por tanto de ozono)
más importante en la atmósfera terrestre. La energía de disociación es
306 kJ/mol. Encontrar la longitud de onda de un fotón capaz de producir
dicha reacción.
- La frecuencia umbral para la emisión fotoeléctrica del cobre es
1.1
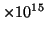 s
s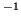 . ¿Cuál será la energía
máxima (en electronvoltios) de los fotoelectrones emitidos cuando la
luz de frecuencia 1.5
. ¿Cuál será la energía
máxima (en electronvoltios) de los fotoelectrones emitidos cuando la
luz de frecuencia 1.5
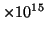 s
s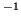 incide sobre una
superficie de cobre?.
incide sobre una
superficie de cobre?.
- El potencial de extracción del sodio es 2.3 eV:
a) ¿cuál será la máxima longitud de onda de la luz, que producirá
emisión de fotoelectrones en el sodio? y
b) ¿cuál será la energía
cinética máxima de los fotoelectrones si luz de 2000 Å
incide sobre una superficie de sodio?.
- La función trabajo del K es 2.2 eV y la del Ni 5.0 eV.
(a) Calcular las frecuencias y longitudes de onda
umbral para estos dos metales. (b) ¿Dará lugar la luz ultravioleta de
longitud de onda 400 nm al efecto fotoeléctrico en el K? ¿Y en el Ni?
(c) Calcular la máxima energía cinética de los electrones emitidos en
(b).
- Cuando se ilumina una cierta superficie metálica con luz de
diferentes longitudes de onda y se miden los potenciales que detienen los
fotoelectrones, se obtienen los valores que se muestran en la siguiente
tabla:
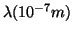 |
3.66 |
4.05 |
4.36 |
4.92 |
5.46 |
5.79 |
| V(V) |
1.48 |
1.15 |
0.93 |
0.62 |
0.36 |
0.24 |
Representando el potencial en función de la frecuencia,
determinar: (a) la frecuencia umbral,
(b) el potencial de extracción del metal, y
(c) la constante de Planck.
- Cuando cierto metal se irradia con luz de frecuencia
3.0
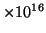 s
s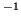 , los fotoelectrones emitidos
tienen una energía cinética doce veces mayor que los fotoelectrones
emitidos cuando el mismo metal se irradia con luz de frecuencia
2.0
, los fotoelectrones emitidos
tienen una energía cinética doce veces mayor que los fotoelectrones
emitidos cuando el mismo metal se irradia con luz de frecuencia
2.0
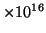 s
s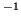 ¿Cuál será la frecuencia
umbral del metal?.
¿Cuál será la frecuencia
umbral del metal?.
- En un tubo de rayos X donde los electrones se aceleran con un
potencial de 5000 V, la mínima longitud de onda de los rayos X
producidos es 248 pm. Estimad el valor de la constante de Planck.
- Calcular la frecuencia hacia la cual convergen todas las líneas
espectrales de la serie de Lyman. ¿Cuál será la longitud de
onda y la energía de esta radiación?.
- Calcular la longitud de onda en Angstrom y la frecuencia en
s
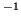 de la primera línea de la serie de Balmer.
de la primera línea de la serie de Balmer.
- Calcular el potencial de ionización del átomo de hidrógeno cuando
el electrón ocupa la órbita con número cuántico principal igual a 5.
- Calcular la longitud de onda de De Broglie asociada a:
(a) un electrón con 15 keV de energía cinética,
(b) un protón con 15 keV de energía cinética,
(c) una molécula de SF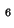 a una velocidad de
1 m/s, y
(d) un objeto de 1 kg a una velocidad de 1 m/s.
a una velocidad de
1 m/s, y
(d) un objeto de 1 kg a una velocidad de 1 m/s.
- Calcular el módulo de (a)
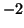 , (b)
, (b) 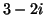 , (c)
, (c)
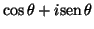 , (d)
, (d) 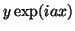 .
.
- Probar que
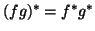 donde
donde 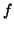 y
y 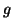 son cantidades
complejas.
son cantidades
complejas.
- Verificar que si
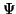 es una solución de la ecuación de
Schrödinger dependiente del tiempo, entonces
es una solución de la ecuación de
Schrödinger dependiente del tiempo, entonces 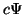 es también
solución siendo
es también
solución siendo 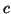 una constante.
una constante.
- Comprobar que las funciones
![$\Psi(x,t) = A \exp[2\pi i
(\pm x/\lambda -\nu t)]$](img20.gif) son soluciones de la ecuación de Schrödinger
monodimensional dependiente del tiempo
de una partícula libre. Suponiendo que
son soluciones de la ecuación de Schrödinger
monodimensional dependiente del tiempo
de una partícula libre. Suponiendo que 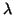 es la longitud de
onda de De Broglie, expresar
es la longitud de
onda de De Broglie, expresar 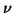 en función del momento lineal
en función del momento lineal 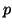 .
.
- Si la posición de un electrón se mide con una precisión de
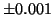 Å ¿Cuál será la máxima precisión para el momento?
Å ¿Cuál será la máxima precisión para el momento?
- Un átomo sufre una transición desde un estado excitado con un
tiempo de vida de 1 ns al estado fundamental, y emite un fotón con una
longitud de onda de 600 nm. Calcular la incertidumbre en la energía del
estado excitado.
- Hallar la longitud de onda de la luz emitida cuando una partícula
de
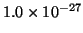 g en una caja monodimensional de 30 nm pasa del
nivel
g en una caja monodimensional de 30 nm pasa del
nivel 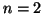 al nivel
al nivel 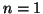 .
.
- Calcular la energía en electronvoltios (eV) de los niveles
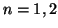 y 3 de un electrón en una caja de potencial monodimensional de
longitud
y 3 de un electrón en una caja de potencial monodimensional de
longitud 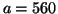 pm.
pm.
- Para una partícula en el estado estacionario
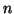 de una caja
monodimensional de longitud
de una caja
monodimensional de longitud 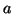 , encontrar la probabilidad de que la
partícula esté en la región
, encontrar la probabilidad de que la
partícula esté en la región
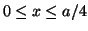 .
.
- Para el estado fundamental de una partícula en una caja
monodimensional de longitud
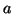 , encontrar la probabilidad de que la
partícula esté entre
, encontrar la probabilidad de que la
partícula esté entre 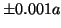 del punto
del punto 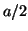 .
Calcular el valor medio de la posición y el momento.
.
Calcular el valor medio de la posición y el momento.
- Para el estado estacionario de número cuántico
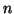 de la partícula
en una caja, escribir una expresión para la probabilidad de que la
partícula se encuentre entre
de la partícula
en una caja, escribir una expresión para la probabilidad de que la
partícula se encuentre entre 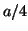 y
y 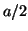 .
.
- Para un electrón en una determinada caja monodimensional, la
transición observada de menor frecuencia es
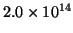 s
s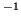 . Calcular la longitud de la caja.
. Calcular la longitud de la caja.
- Teniendo en cuenta las condiciones de continuidad que la función
de onda debe satisfacer, que pasaría a los niveles de energía de una
partícula en una caja monodimensional si la longitud de la caja cambia
de
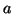 a
a 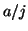 (
(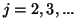 ).
).
- Encontrar las funciones de onda y las correspondientes energías
para los estados estacionarios de una partícula en una caja de potencial
tridimensional de lados
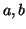 y
y 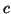 .
.
- Para una partícula en una caja cúbica de lado
 : (a) ¿Cuántos
estados tienen energías en el rango de 0 a
: (a) ¿Cuántos
estados tienen energías en el rango de 0 a 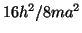 ? (b) ¿Cuántos
niveles de energía caen en ese rango?.
? (b) ¿Cuántos
niveles de energía caen en ese rango?.
- Para una partícula en una caja tridimensional de lados
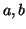 y
y
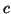 con
con 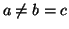 , hacer una tabla de
, hacer una tabla de 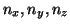 , las energías y
las degeneraciones de los niveles con números cuánticos en el rango de 1
a 5 (Tomar
, las energías y
las degeneraciones de los niveles con números cuánticos en el rango de 1
a 5 (Tomar 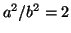 ).
).
- Comprobar que la función
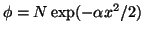 es
solución de la ecuación de Schrödinger para un oscilador armónico.
Relacionar
es
solución de la ecuación de Schrödinger para un oscilador armónico.
Relacionar 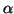 con la constante de fuerza del oscilador y la masa
de la partícula, y calcular la energía correspondiente a esa solución.
Calcular el valor medio de la posición de la partícula.
con la constante de fuerza del oscilador y la masa
de la partícula, y calcular la energía correspondiente a esa solución.
Calcular el valor medio de la posición de la partícula.
- La molécula
 tiene una constante de fuerza de enlace de 314
Nm
tiene una constante de fuerza de enlace de 314
Nm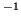 . Calcular para
. Calcular para 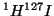 y
y 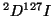 : (a) La frecuencia
vibracional clásica en s
: (a) La frecuencia
vibracional clásica en s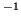 , (b) el número de onda correspondiente a
la transición de
, (b) el número de onda correspondiente a
la transición de 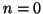 a
a 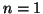 en el espectro vibracional.
en el espectro vibracional.
- Calcular la frecuencia de la radiación emitida cuando un
oscilador armónico de frecuencia 6.0
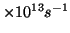 salta del
nivel
salta del
nivel 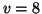 al
al 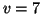 .
.
- Dada la función de onda normalizada para una partícula que se
mueve en una dimensión
- Comprobar si existe algún valor de
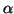 para el cual esta
función es solución de la ecuación de
Schrödinger para un oscilador armónico monodimensional de masa
para el cual esta
función es solución de la ecuación de
Schrödinger para un oscilador armónico monodimensional de masa 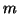 y
constante de fuerza
y
constante de fuerza 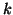 .
.
- Obtener la densidad de probabilidad en
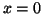 .
.
- Calcular las posiciones de los máximos de la densidad de probabilidad
en función de
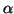 .
.
- Un oscilador armónico tridimensional tiene un potencial
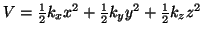 , donde las tres constantes de
fuerza no son necesariamente iguales. Escribir una expresión para los
niveles de energía de este sistema ¿Cuál es el punto cero de energía?
, donde las tres constantes de
fuerza no son necesariamente iguales. Escribir una expresión para los
niveles de energía de este sistema ¿Cuál es el punto cero de energía?
- Expresar
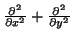 en coordenadas polares.
en coordenadas polares.
- Mostrar que si
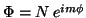 es una función definida
entre 0 y 2
es una función definida
entre 0 y 2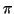 , la constante de normalización
, la constante de normalización 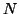 vale
vale
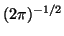 .
.
- Calcular la energía electrostática de dos electrones separados
3.0 Å en el vacío. Expresar la respuesta en Julios, ergios y eV.
- ¿Existe una atracción gravitatoria entre el electrón y el
protón en el átomo de hidrógeno? Si existe ¿por qué no se tiene en
cuenta en el Hamiltoniano? Hacer un cálculo para justificar la
respuesta.
- a) Supongamos
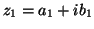 y
y
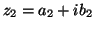 , donde
, donde
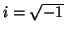 y los coeficientes
y los coeficientes 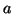 y
y 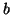 son reales. Si
son reales. Si 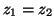 ,
indicar que condiciones tienen que cumplir los coeficientes
,
indicar que condiciones tienen que cumplir los coeficientes 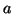 y
y 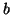 .
.
b) Verifique que para la función
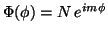 el requisito
el requisito
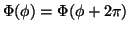 conduce a la
condición de que
conduce a la
condición de que 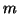 sea un número entero.
sea un número entero.
- Usar la energía de ionización del H para predecir la de los
iones He
 , Li
, Li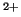 y U
y U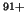 .
.
- Calcular la longitud de onda del fotón emitido cuando un
electrón salta del nivel
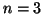 al
al 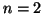 de un átomo hidrogenoide.
Indicar para que estados es posible este salto.
de un átomo hidrogenoide.
Indicar para que estados es posible este salto.
- Ya que los átomos de H y D poseen distinta masa reducida, existirán
pequeñas diferencias de energías entre sus niveles. Calcular los
potenciales de ionización y la longitud de onda de la primera línea de
la serie de Balmer para los dos isótopos.
- Un átomo hidrogenoide tiene una serie de líneas espectrales a
26.2445, 19.4404, 17.3578 y 16.4028 nm. Calcular la carga
nuclear del átomo y describir a qué transiciones corresponden cada una
de las líneas espectrales.
- ¿Cuáles de las siguientes transiciones están permitidas en el
espectro electrónico de un átomo hidrogenoide?
(a)
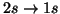 (b)
(b)
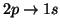 (c)
(c)
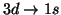 (d)
(d)
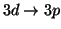
- Demostrar que el máximo de la función de distribución radial
para el estado fundamental de un átomo hidrogenoide está en
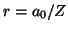 .
Encontrar los valores numéricos para C
.
Encontrar los valores numéricos para C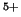 y B
y B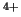 .
.
- Calcular la probabilidad de que el electrón en el estado 1s del
átomo de hidrógeno esté a una distancia del núcleo entre 0 y 2.0 Å
- Comprobar que la constante de normalización
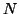 del orbital 1s:
del orbital 1s:
![$\phi_{1s}=N\exp[-Zr/a_0]$](img83.gif) es
es
![$N= [\frac{Z^3}{\pi a_0^3}]^{1/2}$](img84.gif)
- La función de onda normalizada del orbital
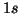 de un átomo
hidrogenoide es:
de un átomo
hidrogenoide es:
- Determinar el valor medio de la distancia del núcleo al
electrón para el orbital 1s del átomo de H y del ion He
 .
.
- Comparar los resultados del apartado anterior con el valor del
máximo de la función de distribución radial.
- Determinar el valor medio de la energía potencial en ambos
sistemas.
- Dado el siguiente orbital del átomo de hidrógeno:
- Encontrar sus números cuánticos y decir de que orbital se trata.
- Usando los resultados del apartado anterior,
decir cuánto vale el módulo del momento angular del
electrón cuando está en este estado.
- Decir cuánto vale la proyección sobre el eje z del
momento angular del electrón cuando está en este estado.
- Encontrar sus planos nodales.
- Comprobar que su constante de normalización vale
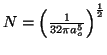
- Calcular el valor más probable
de la distancia entre el electrón y el núcleo.
- Calcular la probabilidad de hallar el electrón entre los
valores de
 y
y 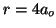 .
.
- Calcular el valor medio de
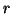 y de la energía potencial.
y de la energía potencial.
- Calcular la probabilidad de hallar el electrón
entre los valores de
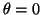 y
y
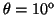 .
.
- Calcular la probabilidad de hallar el electrón
entre los valores de
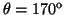 y
y
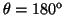 .
.
- Calcular la probabilidad de hallar el electrón
entre los valores de
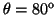 y
y
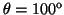 .
.
- Evaluar la densidad de probabilidad en los
puntos
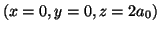 y
y
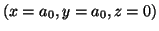 .
.
- Comprobar que la función
![$f(r,\theta)=Nr\exp[-Zr/2a_0]\cos\theta$](img100.gif) es solución de la ecuación de Schrödinger para un átomo hidrogenoide
y obtener la energía de esta función.
es solución de la ecuación de Schrödinger para un átomo hidrogenoide
y obtener la energía de esta función.
- Establecer si cada una de estas funciones es simétrica,
antisimétrica o ni una cosa ni la otra
(a) 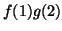 (b)
(b) 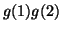 (c)
(c)
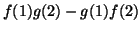 (d)
(d)
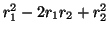 (e)
(e)
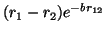
donde 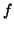 y
y 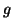 son funciones arbitrarias de las coordenadas de las
partículas idénticas 1 y 2,
son funciones arbitrarias de las coordenadas de las
partículas idénticas 1 y 2, 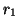 ,
, 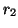 son las distancias de las
partículas al núcleo y
son las distancias de las
partículas al núcleo y 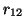 la distancia entre las dos.
la distancia entre las dos.
- Tomando
demostrar que
(a) el intercambio de 2 columnas cambia el signo de 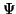 ,
,
(b) el intercambio de 2 filas cambia el signo de 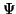 ,
,
(c) los dos electrones no pueden estar en el mismo espín-orbital.
- Mostrar que la siguiente función de onda para el átomo de
helio es antisimétrica con respecto al intercambio de los dos
electrones
- Los primeros potenciales de ionización del Na, K y Rb
son 5.138, 4.341
y 4.166 eV, respectivamente. Suponiendo que el nivel de energía del
electrón mas externo puede representarse por la energía de los
orbitales hidrogenoides con una carga nuclear efectiva
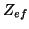 , y que
los orbitales importantes son los 3s, 4s y 5s, respectivamente,
calcular
, y que
los orbitales importantes son los 3s, 4s y 5s, respectivamente,
calcular 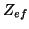 para estos átomos
para estos átomos
- Escriba el hamiltoniano para el movimiento interno del átomo de
Li.
- Dados los orbitales atómicos
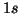 y
y 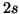 del átomo de Be,
construir el determinante de Slater para el estado fundamental.
del átomo de Be,
construir el determinante de Slater para el estado fundamental.
- Deducir el término espectral para el estado fundamental
correspondiente a las configuraciones
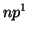
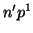 ,
, 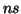
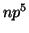 ,
, 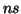
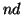 ,
, 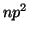 ,
,
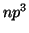 ,
, 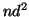 , teniendo en cuenta las reglas de Hund.
, teniendo en cuenta las reglas de Hund.
- Deducir el término espectral para el estado fundamental de los
átomos de He, Li, Be, B, C, N, O y F.
- Deducir los términos espectrales posibles de las configuraciones:
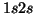 del átomo de He
del átomo de He
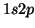 del átomo de He
del átomo de He
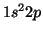 del átomo de Li
del átomo de Li
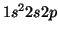 del átomo de Be
del átomo de Be
- Calcular la energía de repulsión nuclear para la molécula de
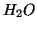 dadas las siguientes coordenadas cartesianas nucleares
dadas las siguientes coordenadas cartesianas nucleares
| Átomo |
x/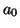 |
y/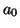 |
z/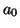 |
| |
|
|
|
| O |
0 |
0 |
0 |
| H |
-1.2 |
-1. |
0 |
| H |
1.2 |
-1. |
0 |
- Calcular la energía de repulsión nuclear para la molécula de
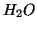 dadas las siguientes coordenadas internas nucleares
dadas las siguientes coordenadas internas nucleares
| Coordenada interna |
|
| |
|
| R(OH) |
0.958 Å |
 |
104.5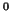 |
- El primer estado excitado del
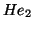 se obtiene excitando un
electrón del OM antienlazante
se obtiene excitando un
electrón del OM antienlazante 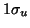 al OM enlazante
al OM enlazante 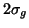 .
Escribe la configuración electrónica. ¿Cuales son las posibles
funciones de onda incluyendo el espín? ¿Cual es el orden de enlace?
Indicar si los estados electrónicos son
.
Escribe la configuración electrónica. ¿Cuales son las posibles
funciones de onda incluyendo el espín? ¿Cual es el orden de enlace?
Indicar si los estados electrónicos son 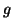 o
o 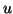 .
.
- Describir el estado electrónico fundamental y la multiplicidad,
utilizando las configuraciones electrónicas, de las siguientes
especies:
a) 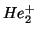 ,
b)
,
b) 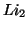 ,
c)
,
c) 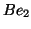 ,
d)
,
d) 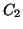 ,
e)
,
e) 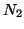 ,
f)
,
f) 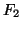 .
.
- Calcular la densidad de probabilidad electrónica en el punto
medio de los hidrógenos en el
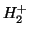 para los estados descritos por
para los estados descritos por
a)
 ,
b)
,
b)
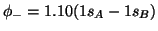
para la distancia internuclear 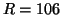 pm.
pm.
- Aplicando la teoría de orbitales moleculares, indíquese cuál de
las siguientes moléculas,
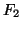 ,
, 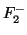 y
y 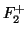 , tendrá
mayor energía de disociación.
, tendrá
mayor energía de disociación.
- Dibujar el diagrama de niveles de energía de la molécula de
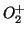 .
Determinar su estructura electrónica y justificar que su estado
fundamental es
.
Determinar su estructura electrónica y justificar que su estado
fundamental es 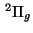 .
.
- Deducir el término espectral más estable correspondiente a
cada una de las siguientes configuraciones electrónicas de
moléculas
diatómicas homonucleares:
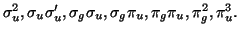
- Dadas las curvas de energía potencial para las moléculas
diatómicas
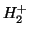 y
y 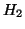 , calcular la energía de disociación del
, calcular la energía de disociación del
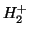 (
(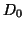 ) sabiendo que la energía de disociación del
) sabiendo que la energía de disociación del 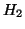 es
es
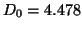 eV y que el potencial de ionización del
eV y que el potencial de ionización del 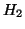 es
es
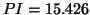 eV.
eV.
![\includegraphics[angle=0,scale=0.5]{fqcfig1.ps}](H2.gif)
- Calcular
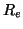 ,
, 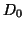 ,
, 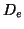 para las moléculas diatómicas
para las moléculas diatómicas 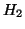 y
y
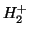 de la gráfica anterior, así como el PI del
de la gráfica anterior, así como el PI del 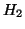 .
.
- En la siguiente figura se representa la superficie de energía
potencial para la reacción colineal
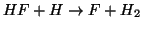 .
Indicar cuáles son los reactivos, productos, estado de transición y
dibujar cualitativamente el camino de mínima energía.
.
Indicar cuáles son los reactivos, productos, estado de transición y
dibujar cualitativamente el camino de mínima energía.
![\includegraphics[angle=0,scale=0.5]{fqcfig2.ps}](FH2.gif)
![]() a una velocidad de
1 m/s, y
(d) un objeto de 1 kg a una velocidad de 1 m/s.
a una velocidad de
1 m/s, y
(d) un objeto de 1 kg a una velocidad de 1 m/s.
![\begin{figure}\setlength{\unitlength}{1.cm}%%
\begin{picture}(10,5)(0,0)
\put(1....
...0){$a$}}
\put(12.3,4.5){\makebox(0,0)[l]{$\psi_3(x)$}}
\end{picture}\end{figure}](img30.gif)
![\begin{figure}\setlength{\unitlength}{1.cm}%%
\begin{picture}(10,5)(0,0)
\put(1....
...t(12.3,4.5){\makebox(0,0)[l]{$\vert\psi_3(x)\vert^2$}}
\end{picture}\end{figure}](img31.gif)
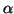 para el cual esta
función es solución de la ecuación de
Schrödinger para un oscilador armónico monodimensional de masa
para el cual esta
función es solución de la ecuación de
Schrödinger para un oscilador armónico monodimensional de masa 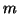 y
constante de fuerza
y
constante de fuerza 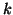 .
.
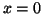 .
.
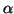 .
.
![]() el requisito
el requisito
![]() conduce a la
condición de que
conduce a la
condición de que ![]() sea un número entero.
sea un número entero.
![]() (b)
(b)
![]() (c)
(c)
![]() (d)
(d)
![]()
 .
.
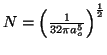
 y
y 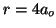 .
.
 y de la energía potencial.
y de la energía potencial.
 y
y
 .
.
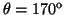 y
y
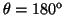 .
.
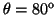 y
y
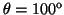 .
.
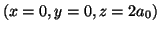 y
y
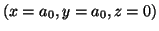 .
.
![]() (b)
(b) ![]() (c)
(c)
![]() (d)
(d)
![]() (e)
(e)
![]()
![]() y
y ![]() son funciones arbitrarias de las coordenadas de las
partículas idénticas 1 y 2,
son funciones arbitrarias de las coordenadas de las
partículas idénticas 1 y 2, ![]() ,
, ![]() son las distancias de las
partículas al núcleo y
son las distancias de las
partículas al núcleo y ![]() la distancia entre las dos.
la distancia entre las dos.
![]() ,
,
![]() ,
,
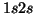 del átomo de He
del átomo de He
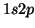 del átomo de He
del átomo de He
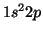 del átomo de Li
del átomo de Li
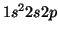 del átomo de Be
del átomo de Be
![]() ,
b)
,
b) ![]() ,
c)
,
c) ![]() ,
d)
,
d) ![]() ,
e)
,
e) ![]() ,
f)
,
f) ![]() .
.
![]() ,
b)
,
b)
![]()
![]() pm.
pm.
![\includegraphics[angle=0,scale=0.5]{fqcfig1.ps}](H2.gif)
![\includegraphics[angle=0,scale=0.5]{fqcfig2.ps}](FH2.gif)