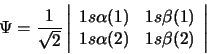Fundamentos de Química Cuántica, 1 de Química.
(Septiembre 1998, Modelo 1)
de Química.
(Septiembre 1998, Modelo 1)
Puntuación:

- Cada respuesta correcta suma 1/2 punto.
- Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
- Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya
respuesta se conozca con seguridad. Sólo hay una respuesta correcta en
cada pregunta.
En la hoja de respuestas no olvidéis rellenar:
- el nombre y apellidos.
- el DNI.
- el MODELO (Importante: toda hoja de respuestas sin modelo
equivale a un suspenso).
- Según la hipótesis de De Broglie, a igualdad de velocidad...
- la longitud de onda asociada al movimiento de un electrón será
menor que la asociada al de un protón.
- la longitud de onda asociada al movimiento de un protón será
menor que la asociada al de un electrón.
- las longitudes de onda asociadas a los movimiento de un protón
y de un electrón serán iguales.
- las longitudes de onda asociadas a los movimiento de un protón
y de un electrón tendrán signos opuestos debido al signo de las cargas
de ambos.
- Las propiedades ondulatorias se hacen más patentes
- entre dos partículas con igual masa, para aquélla cuya velocidad sea
menor.
- entre dos partículas con igual velocidad, para aquella cuya masa sea mayor.
- no depende de la masa de la partícula.
- cuanto mayor sea la energía cinética de la partícula.
- Suponga que se desea medir simultáneamente la posición,
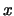 , y el
momento,
, y el
momento, 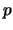 , de un electrón con una precisión
, de un electrón con una precisión 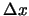 y
y
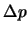 , respectivamente, sabiendo que
, respectivamente, sabiendo que
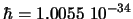 J s.
J s.
- Se pueden medir ambas magnitudes simultáneamente con tanta
exactitud como se desee.
- No se pueden medir ambas magnitudes en ningún caso.
- Se pueden medir si
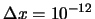 m y
m y
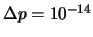 kg m / s.
kg m / s.
- Se pueden medir si
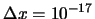 m y
m y
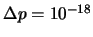 kg m / s.
kg m / s.
- La parte espacial de la función de onda de un sistema de N
partículas:
- depende de 3N coordenadas espaciales.
- depende de N coordenadas espaciales.
- no depende de las coordenadas espaciales.
- depende de 4N coordenadas espaciales.
- La densidad de probabilidad de una función
de onda monodimensional para una partícula tiene las siguientes
unidades:
- adimensional.
- longitud elevada a -1.
- longitud elevada a -2.
- longitud elevada a +2.
- Si el hamiltoniano de un sistema de dos partículas,
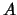 y
y 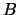 , se
puede escribir como suma de dos hamiltonianos, cada uno de los cuales
depende de las coordenadas de una sola partícula:
, se
puede escribir como suma de dos hamiltonianos, cada uno de los cuales
depende de las coordenadas de una sola partícula:
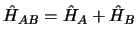 , y
, y 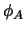 y
y 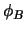 cumplen
cumplen
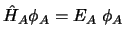 y
y
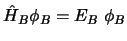 , entonces ...
, entonces ...
-
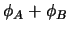 representa un estado estacionario del sistema
completo.
representa un estado estacionario del sistema
completo.
-
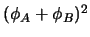 representa un estado estacionario del
sistema completo.
representa un estado estacionario del
sistema completo.
-
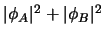 representa un estado estacionario del
sistema completo.
representa un estado estacionario del
sistema completo.
-
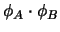 representa un estado estacionario del
sistema completo.
representa un estado estacionario del
sistema completo.
- Para los distintos estados de la partícula en la caja monodimensional,
- La densidad de probabilidad de la partícula en los extremos
de la caja es independiente del número cuántico n.
- La densidad de probabilidad de la partícula en el centro
de la caja es independiente del número cuántico n.
- El número de puntos donde la densidad de probabilidad
de la partícula es máxima disminuye al aumentar n.
- En el centro de la caja la densidad de probabilidad de la
partícula depende del valor de n pero siempre es un máximo.
- Si en una caja cúbica (de dimensiones
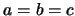 ) se produce una
transformación que alarga uno de los lados (p. ej.
) se produce una
transformación que alarga uno de los lados (p. ej. 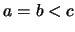 )...
)...
- se rompe completamente la degeneración de todos los estados
que estaban inicialmente degenerados en energía.
- se rompe la degeneración de algunos estados
inicialmente degenerados.
- el proceso no afecta a la degeneración de los estados.
- no ocurre nada con la degeneración de los estados ya que en la
caja cúbica no hay estados degenerados.
- En el oscilador ármonico monodimensional la probabilidad de encontrar
a la partícula en las regiones del espacio no comprendidas entre
los puntos de retorno clásico:
- es nula ya que la energía cinética es menor que cero.
- es nula ya que la energía potencial es menor que cero.
- es negativa.
- no es nula.
- En el efecto túnel, una partícula puede atravesar una región
clásicamente prohibida...
- adquiriendo una energía extra procedente de la barrera.
- saltando por encima de la barrera.
- sin que cambie su energía.
- porque la energía es oscilante.
- En el átomo de hidrógeno (modelo electrostático)...
- los orbitales
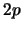 tienen más energía que los
tienen más energía que los 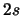 .
.
- los orbitales
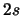 tienen más energía que los
tienen más energía que los 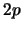 .
.
- los orbitales
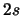 tienen la misma energía que los
tienen la misma energía que los 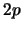 .
.
- los orbitales
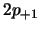 y
y 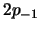 tienen más energía que los
tienen más energía que los
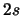 y
y 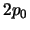 .
.
- Para el átomo de He la función:
- es la única función válida para cualquier estado del He.
- describe una función aproximada del estado fundamental del He.
- es una solución exacta de la ecuación de Schrödinger
independiente del tiempo.
- se anula ya que hay dos filas iguales.
- La función de espín
para un sistema de dos electrones:
- es simétrica respecto al intercambio de partículas.
- es antisimétrica respecto al intercambio de partículas.
- es simétrica y antisimétrica respecto al intercambio de
partículas.
- no tiene simetría respecto al intercambio de partículas.
- Una función de onda aproximada y aceptable para un
estado electrónico excitado de la molécula H
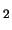 es:
es:
-
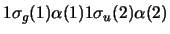
-
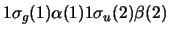
-
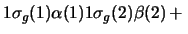
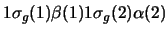
-
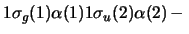
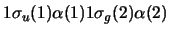
- El orden de enlace de la molécula de H
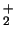 es 1/2 y su
energía de disociación 2.8 eV. Para la molécula de Li
es 1/2 y su
energía de disociación 2.8 eV. Para la molécula de Li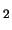 el
orden de enlace es 1 y la energía de disociación 1.1 eV.
el
orden de enlace es 1 y la energía de disociación 1.1 eV.
- La molécula de Li
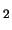 es más estable que la de H
es más estable que la de H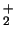 .
.
- La molécula de Li
 es menos estable que la de H
es menos estable que la de H .
.
- La molécula de H
 no se forma al tener orden de enlace 1/2.
no se forma al tener orden de enlace 1/2.
- No podemos saber cuál es más estable de las dos moléculas.
- El Hamiltoniano electrónico de la molécula Li
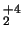 , donde
los subíndices 1 y 2 se refieren a los electronesy A y B a los átomos,
es:
, donde
los subíndices 1 y 2 se refieren a los electronesy A y B a los átomos,
es:
-
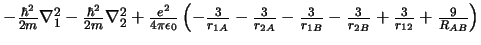
-
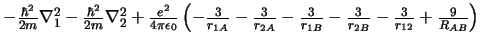
-
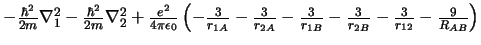
-
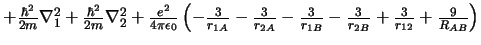
- La función trabajo de cierto metal es
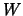 . Cuando
incide sobre la superficie de este metal radiación de longitud
de onda
. Cuando
incide sobre la superficie de este metal radiación de longitud
de onda 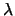 , la energía cinética
, la energía cinética 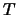 de los electrones
emitidos es:
de los electrones
emitidos es:
-
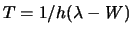
-
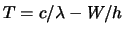
-
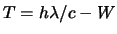
-
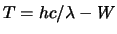
- La ecuación
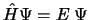 implica...
implica...
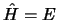 .
.
- que la energía potencial no depende explícitamente del tiempo.
- que la energía total E, depende de la posición.
- que la energía potencial no depende de la posición ni del tiempo.
- La cuantización de la energía en el sistema formado por una
partícula en una caja...
- aparece al normalizar la función de onda.
- es consecuencia de la continuidad de la función de onda.
- es consecuencia de la continuidad de las
derivadas primeras de la función de onda.
- sólo se da en cajas monodimensionales.
- En una molécula diatómica homonuclear...
- todos los orbitales g son siempre enlazantes y todos los
u son antienlazantes.
- los orbitales
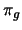 son enlazantes y los
son enlazantes y los 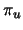 son
antienlazantes.
son
antienlazantes.
- los orbitales
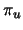 son enlazantes y los
son enlazantes y los 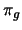 son
antienlazantes.
son
antienlazantes.
- no tiene sentido hablar de orbitales g y u.
© Copyright.
Cristina Sanz Sanz
2001-10-10