Examen de Fundamentos de Química Cuántica (96/97)
 1
1 de C. Químicas.
de C. Químicas.
Puntuación: 
- Cada respuesta correcta suma 1/2 punto.
- Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
- Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya
respuesta se conozca con seguridad. Sólo hay una respuesta correcta en
cada pregunta.
En la hoja de respuestas no olvidéis rellenar:
- el nombre y apellidos.
- el DNI.
- el MODELO (Importante: toda hoja de respuestas sin modelo
equivale a un suspenso).
- Un átomo excitado puede volver al estado fundamental de dos
maneras. En la primera, pasa a un estado intermedio emitiendo
radiación de frecuencia
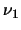 , y después
al estado fundamental emitiendo radiación de frecuencia
, y después
al estado fundamental emitiendo radiación de frecuencia
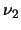 .
En la segunda pasa directamente al estado fundamental
emitiendo radiación de frecuencia
.
En la segunda pasa directamente al estado fundamental
emitiendo radiación de frecuencia 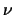 .
¿Cuál será la relación entre
.
¿Cuál será la relación entre 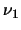 ,
, 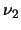 y
y 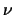 ?
?
-
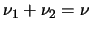
-
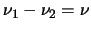
-
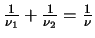
-
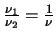
- La función trabajo de un metal es 3.4 eV. Se puede extraer un electrón
mediante el efecto fotoeléctrico si se hace incidir sobre el metal:
- un fotón de energía 3.5 eV.
- un fotón de energía 1.8 eV.
- dos fotones de energía 1.8 eV cada uno.
- un número suficientemente grande de fotones independientemente
de su energía.
- Suponga que se desea medir simultáneamente la posición,
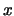 , y el
momento,
, y el
momento, 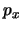 , de un electrón con una exactitud
, de un electrón con una exactitud 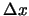 y
y
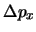 , respectivamente. Sabiendo que
, respectivamente. Sabiendo que
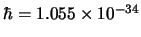 J s,
J s,
- Se pueden medir ambas magnitudes simultáneamente con tanta
exactitud como se desee.
- No se pueden medir ambas magnitudes en ningún caso.
- Es posible obtener en una medida
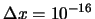 m y
m y
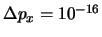 kg m/s.
kg m/s.
- Es posible obtener en una medida
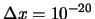 m y
m y
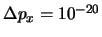 kg m/s.
kg m/s.
- Las propiedades ondulatorias de una partícula se hacen más patentes
- al aumentar su energía cinética.
- al aumentar su velocidad.
- al disminuir su momento lineal.
- al disminuir su longitud de onda de de Broglie.
- Una función de onda aproximada y aceptable para el estado
electrónico fundamental del Be
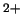 viene dada por:
viene dada por:
-
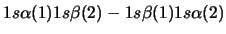
-
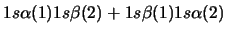
-
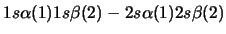
-
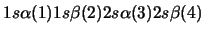
- Un electrón se encuentra en el estado
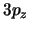 del
átomo de hidrógeno.
del
átomo de hidrógeno.
- La densidad de probabilidad es la misma en todo el espacio.
- La densidad de probabilidad es negativa si la coordenada
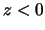 .
.
- La densidad de probabilidad sólo depende de la distancia
entre el electrón y el protón.
- La densidad de probabilidad es mayor a lo largo del eje
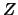 que a
lo largo del eje
que a
lo largo del eje 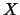 .
.
- La función de onda de
una partícula en una caja monodimensional de longitud
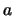 , con paredes
de potencial infinitas, es
, con paredes
de potencial infinitas, es
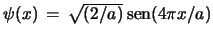 para
para 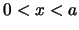 . Cuando la partícula se encuentra en dicho estado:
. Cuando la partícula se encuentra en dicho estado:
- La probabilidad de encontrarla en
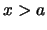 no es nula.
no es nula.
- La densidad de probabilidad en
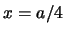 es nula.
es nula.
- La densidad de probabilidad en
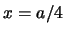 es mayor que en
es mayor que en 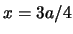 .
.
- La densidad de probabilidad en
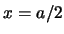 es mayor que en
es mayor que en 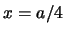 .
.
- El Hamiltoniano electrónico de la molécula LiH
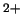 , donde
los subíndices 1 y 2 se refieren a los electrones, es:
, donde
los subíndices 1 y 2 se refieren a los electrones, es:
-
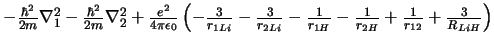
-
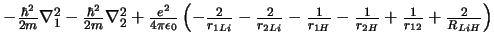
-
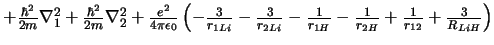
-
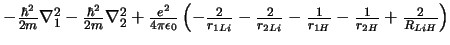
- La densidad de probabilidad de una partícula en un estado
estacionario:
- No depende de las coordenadas espaciales pero sí del tiempo.
- No depende de las coordenadas espaciales ni del tiempo.
- Depende de las coordenadas espaciales pero no del tiempo.
- Depende de las coordenadas espaciales y del tiempo.
- Para una molécula diatómica homonuclear, donde el eje
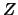 es el eje internuclear y
es el eje internuclear y 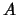 y
y 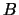 denotan los dos núcleos, decir
cuál de las siguientes afirmaciones es correcta:
denotan los dos núcleos, decir
cuál de las siguientes afirmaciones es correcta:
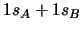 es un orbital
es un orbital 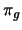 .
.
-
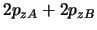 es un orbital
es un orbital 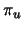 .
.
-
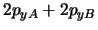 es un orbital
es un orbital 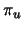 .
.
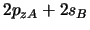 es un orbital
es un orbital 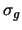 .
.
- Un electrón en un átomo de hidrógeno se encuentra en el nivel
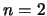 .
.
- Existen estados de diferente energía en ese nivel.
- Todos los estados de ese nivel tienen el mismo valor del momento
angular.
- Todos los estados de ese nivel tienen la misma energía.
- Sólo existe un estado en ese nivel.
- Considere la función de onda del estado fundamental del átomo
de helio:
- La función de onda completa no cambia de signo al intercambiar las
coordenadas de dos electrones.
- La parte espacial de dicha función debe ser antisimétrica
al intercambiar las coordenadas de dos electrones.
- La parte espacial de dicha función debe ser simétrica
al intercambiar las coordenadas de dos electrones.
- La función de onda completa sólo depende de las coordenadas
espaciales.
- Cuál de las siguientes afirmaciones es cierta:
- La aproximación de Born-Oppenheimer se basa en que las velocidades
de los electrones son mucho mayores que las de los núcleos.
- La aproximación de Born-Oppenheimer se basa en que las velocidades
de los electrones son mucho menores que las de los núcleos.
- La aproximación de Born-Oppenheimer se basa en que las velocidades
de electrones y núcleos son muy similares.
- La aproximación de Born-Oppenheimer sólo se puede emplear para
moléculas diatómicas.
- Los orbitales moleculares de la molécula H
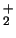 cumplen:
cumplen:
- Son todos antienlazantes.
- No tiene sentido clasificarlos como g o u.
- Su energía es independiente de la distancia internuclear.
- Su energía depende de la distancia internuclear.
- La configuración electrónica del estado
fundamental de la molécula diatómica B
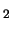 es
es
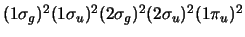 . Teniendo en cuenta el orden de enlace,
decir cuál de las siguientes afirmaciones es correcta:
. Teniendo en cuenta el orden de enlace,
decir cuál de las siguientes afirmaciones es correcta:
- El ion positivo B
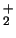 tiene una energía de disociación mayor
que la de la molécula neutra B
tiene una energía de disociación mayor
que la de la molécula neutra B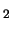 .
.
- El ion positivo B
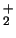 tiene una energía de disociación menor
que la de la molécula neutra B
tiene una energía de disociación menor
que la de la molécula neutra B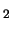 .
.
- El ion negativo B
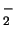 tiene una energía de disociación menor
que la de la molécula neutra B
tiene una energía de disociación menor
que la de la molécula neutra B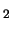 .
.
- Esta molécula es necesariamente inestable.
- Considerar los orbitales moleculares
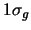 y
y 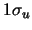 de la molécula de H
de la molécula de H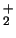 :
:
- Ambos tienen un plano nodal.
- Ninguno de los dos tienen planos nodales.
- El
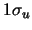 tiene un plano nodal que contiene al eje
internuclear.
tiene un plano nodal que contiene al eje
internuclear.
- El
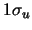 tiene un plano nodal perpendicular al eje
internuclear.
tiene un plano nodal perpendicular al eje
internuclear.
- En átomos hidrogenoides las energías orbitales son:
- Función de los números cuánticos
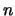 y
y 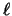 .
.
- Función sólo del número cuántico principal
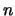 .
.
- Directamente proporcionales al número cuántico
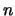 .
.
- Directamente proporcionales al número cuántico
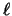 .
.
- ¿Cuál de las siguientes transiciones del espectro
electrónico de un átomo hidrogenoide corresponde a una transición
permitida de la serie de Lyman?:
-
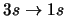
-
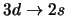
-
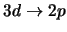
-
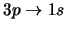
- La energía de disociación (
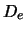 ) de la molécula de H
) de la molécula de H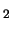 es:
es:
- La suma de la energía de los dos átomos separados y la
energía del mínimo de la curva de energía potencial.
- La diferencia entre la energía de los dos átomos separados
y la energía del mínimo de la curva de energía potencial.
- La suma de la energía del punto cero
y la energía del mínimo de la curva de energía potencial.
- La diferencia entre la energía del punto cero
y la energía del mínimo de la curva de energía potencial.
- La probabilidad de que un átomo de Hidrógeno con una energía
cinética
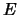 atraviese una barrera de potencial de anchura
atraviese una barrera de potencial de anchura 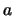 y
altura
y
altura 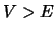 , por efecto túnel:
, por efecto túnel:
- Aumenta si aumentamos la anchura de la barrera
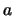 .
.
- Aumenta si aumentamos la altura de la barrera
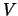 .
.
- Es menor para el isótopo Deuterio que para el Tritio.
- Aumenta si disminuimos la anchura de la barrera
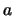 .
.
© Copyright.
Cristina Sanz Sanz
2001-05-17
![]()