Exámen Teórico de Fundamentos de Química Cuántica. (13 de Septiembre de 2007)
Puntuación:
Cada respuesta correcta suma 1/2 punto.
Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya respuesta se conozca con seguridad.
Sólo hay una respuesta correcta en cada pregunta.
- La energía de ionización del Cesio metálico es menor que la correspondiente al Wolframio.
Indica cuál de las siguientes afirmaciones será correcta:
- La longitud de onda crítica (o umbral) para el Cesio es mayor que para el Wolframio.
- La frecuencia crítica (o umbral) del Wolframio es menor que la del Cesio.
- La energía de ionización de estos metales no puede relacionarse con sus propiedades fotoeléctricas.
- Un electrón liberado del Cesio por luz de una cierta frecuencia, tiene una velocidad menor que un electrón liberado del Wolframio por luz de la misma frecuencia.
- La difracción de electrones es una manifestación de:
- La naturaleza corpuscular de la materia.
- La naturaleza ondulatoria de la radiación.
- La naturaleza corpuscular de la radiación.
- La naturaleza ondulatoria de la materia.
- Un electrón que se mueve con un momento lineal o cantidad de movimiento
 :
:
- Lleva una onda asociada cuya longitud de onda vale
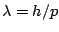 pero no puede medirse
debido al principio de incertidumbre.
pero no puede medirse
debido al principio de incertidumbre.
- Lleva una onda asociada cuya longitud de onda vale
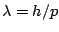 y puede medirse en un
experimento de difracción.
y puede medirse en un
experimento de difracción.
- Lleva una onda asociada cuya longitud de onda vale
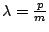 y puede medirse
en un experimento de difracción.
y puede medirse
en un experimento de difracción.
- Lleva una onda asociada cuya longitud de onda vale
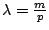 y no puede
medirse debido al principio de incertidumbre.
y no puede
medirse debido al principio de incertidumbre.
- La interpretación de los experimentos de radiación de cuerpo negro ha sido posible tras aceptar:
- Que la energía de la materia está cuantizada.
- El principio de indeterminación.
- El dualismo onda-corpúsculo.
- Que la energía de la radiación electromagnética está cuantizada.
- La función de onda
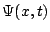 , solución de la ecuación de Schrödinger dependiente del tiempo,
se puede factorizar como el producto de una función espacial por otra que depende del tiempo:
, solución de la ecuación de Schrödinger dependiente del tiempo,
se puede factorizar como el producto de una función espacial por otra que depende del tiempo:
- Si la energía potencial del sistema depende del tiempo.
- Si la energía cinética es constante.
- Si el momento lineal es constante.
- Si la energía potencial del sistema no depende del tiempo.
- ¿Cuál de las siguientes afirmaciones es cierta?
- La posición y el momento lineal de una partícula pueden conocerse con total precisión en
determinadas circunstancias si se dispone del instrumental experimental adecuado.
- La posición o el momento lineal de una partícula nunca se pueden medir.
- La naturaleza ondulatoria de la materia conduce a imprecisiones en la medida simultánea de
la posición y el momento lineal de una partícula.
- El principio de incertidumbre de Heisenberg es una consecuencia de la mecánica clásica
relativista, en concreto del hecho de que
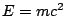 .
.
- La función de onda que describe el estado estacionario de una partícula libre de masa
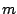 y energía cinética
y energía cinética  ,
moviéndose en el eje
,
moviéndose en el eje 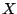 , es
, es
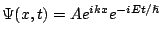 , donde
, donde
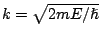 .
La densidad de probabilidad de encontrar a la partícula en un punto del eje
.
La densidad de probabilidad de encontrar a la partícula en un punto del eje 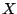 :
:
- Puede ser imaginaria.
- Oscila con la posición
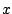 .
.
- No depende de la posición
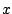 ni del tiempo
ni del tiempo 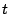 .
.
- No depende de la posición
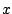 y si depende del tiempo
y si depende del tiempo 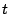 .
.
- El operador mecanocuántico de energía cinética de una partícula,
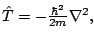 tiene dimensiones de
tiene dimensiones de
- energía
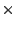 tiempo.
tiempo.
- energía / tiempo.
- energía.
- las mismas unidades que
 .
.
- Un electrón en un átomo de hidrógeno se encuentra en el nivel
 .
.
- Existen estados de diferente energía en ese nivel.
- Todos los estados de ese nivel tienen el mismo valor del momento angular.
- Todos los estados de ese nivel tienen la misma energía.
- Sólo existe un estado en ese nivel.
- La probabilidad de que una partícula de masa
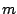 atraviese una barrera de potencial de altura
atraviese una barrera de potencial de altura 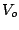 y anchura
y anchura  :
:
- Es independiente de la energía de la partícula.
- Aumenta al disminuir la altura de la barrera.
- Aumenta al aumentar la masa de la partícula.
- Aumenta al aumentar la anchura de la barrera.
- La densidad de probabilidad de un electrón en un átomo hidrogenoide tiene las siguientes dimensiones:
- es adimensional.
- tiene dimensiones de longitud elevada a
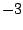 .
.
- tiene dimensiones de tiempo elevado a
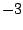 .
.
- tiene dimensiones de longitud elevada a
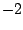 .
.
- La proyección sobre el eje
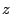 del momento angular de un electrón en el átomo de hidrógeno cuando está en un orbital
del momento angular de un electrón en el átomo de hidrógeno cuando está en un orbital 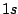 y cuando está en un orbital
y cuando está en un orbital  :
:
- Es
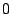 y
y  , respectivamente.
, respectivamente.
- Es
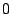 y
y 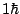 , respectivamente.
, respectivamente.
- Es
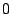 y
y
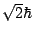 , respectivamente.
, respectivamente.
- No se puede saber cuanto vale en ninguno de los dos casos.
- Una función de onda aproximada y aceptable para el estado electrónico fundamental del Be
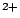 viene dada por:
viene dada por:
-
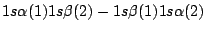
-
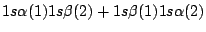
-
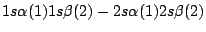
-

- Un determinante de Slater se puede utilizar como función de onda aproximada de un estado de un átomo
multielectrónico porque es una función que:
- cambia de signo cuando se intercambian dos electrones.
- no cambia de signo cuando se intercambian dos electrones.
- permite diferenciar o discernir un electrón del otro.
- no tiene en cuenta el espín de los electrones.
- ¿Cuál de las siguientes transiciones entre orbitales de un átomo hidrogenoide corresponde a una
transición permitida de la serie de Balmer?
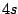
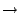
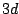
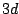
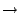
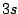
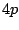
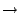

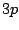
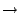
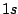
- Cuál de las siguientes afirmaciones es cierta:
- La aproximación de Born-Oppenheimer se basa en que las velocidades de los electrones son
mucho mayores que las de los núcleos.
- La aproximación de Born-Oppenheimer se basa en que las velocidades de los electrones son
mucho menores que las de los núcleos.
- La aproximación de Born-Oppenheimer se basa en que las velocidades de electrones y núcleos
son muy similares.
- La aproximación de Born-Oppenheimer se basa en que la interacción electrón-electrón es mayor que la
interacción nucleo-nucleo.
- El orbital molecular
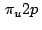 es enlazante porque:
es enlazante porque:
- es un orbital degenerado.
- disminuye la densidad electrónica en la zona internuclear, respecto a los átomos separados.
- aumenta la densidad electrónica en la zona internuclear, respecto a los átomos separados.
- posee un plano nodal perpendicular al eje internuclear.
- La función de onda para el primer estado excitado de un oscilador armónico monodimensional es de la
forma:
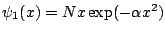
- la función de onda toma el mismo valor en los puntos
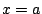 y
y 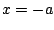 .
.
- la función de onda es máxima en
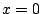 .
.
- la densidad de probabilidad es máxima en
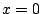 .
.
- la densidad de probabilidad es nula en
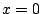 .
.
- Los orbitales reales
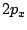 y
y  de los átomos hidrogenoides (que son combinaciones lineales de
los
de los átomos hidrogenoides (que son combinaciones lineales de
los 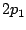 y
y  ):
):
- Son funciones propias de los operadores
 y
y 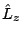
- Sólo son funciones propias de

- Son funciones propias de los operadores
 y
y 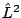
- No son funciones propias ni de
 ni de
ni de 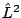 ni de
ni de 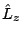
- El Hamiltoniano electrónico de la molécula Li
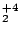 , donde los subíndices 1 y 2 se refieren a los electronesy A y B a los átomos, es:
, donde los subíndices 1 y 2 se refieren a los electronesy A y B a los átomos, es:
-

-

-
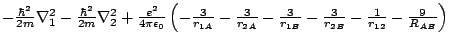
-
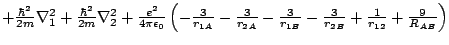
© Copyright.
Universidad Autónoma de Madrid, Departamento de Química Física Aplicada
18-08-2008
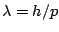 pero no puede medirse
debido al principio de incertidumbre.
pero no puede medirse
debido al principio de incertidumbre.
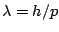 y puede medirse en un
experimento de difracción.
y puede medirse en un
experimento de difracción.
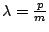 y puede medirse
en un experimento de difracción.
y puede medirse
en un experimento de difracción.
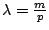 y no puede
medirse debido al principio de incertidumbre.
y no puede
medirse debido al principio de incertidumbre.
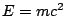 .
.
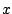 .
.
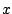 ni del tiempo
ni del tiempo 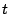 .
.
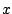 y si depende del tiempo
y si depende del tiempo 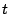 .
.
 tiempo.
tiempo.
 .
.
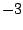 .
.
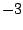 .
.
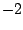 .
.
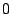 y
y  , respectivamente.
, respectivamente.
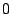 y
y 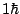 , respectivamente.
, respectivamente.
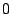 y
y
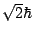 , respectivamente.
, respectivamente.
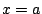 y
y 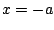 .
.
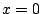 .
.
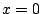 .
.
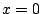 .
.  y
y 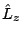

 y
y 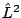
 ni de
ni de 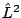 ni de
ni de