Puntuación:

- Cada respuesta correcta suma 1/2 punto.
- Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
- Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya
respuesta se conozca con seguridad. Sólo hay una respuesta correcta en
cada pregunta.
En la hoja de respuestas no olvidéis rellenar:
- NOMBRE Y APELLIDOS.
- DNI.
- MODELO (Importante: toda hoja de respuestas sin modelo
equivale a un suspenso).
- Si podemos escribir la función de onda como
la energía del sistema mecanocuántico se puede expresar
como
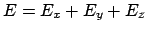
- siempre.
- si
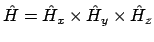 .
.
- si
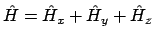 .
.
- si
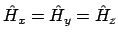 .
.
- Sea
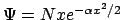 una función de onda válida
para un oscilador armónico monodimensional.
una función de onda válida
para un oscilador armónico monodimensional.
- La función de onda es mínima para
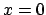 .
.
- La función densidad de probabilidad se anula para
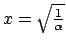 .
.
- La función densidad de probabilidad es mínima para
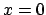 .
.
- La función de onda tiene el mismo valor para
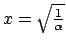 que para
que para
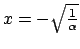
- La curva de energía electrónica frente a R (distancia internuclear)
obtenida usando la aproximación Bohr-Oppenheimer para una
molécula diatómica A-B
- nunca puede tener un mínimo para un estado electrónico excitado.
- presenta un mínimo para el estado fundamental si la molécula es estable.
- presenta un máximo a la distancia de equilibrio para el estado fundamental.
- presenta un mínimo cuando el estado es antienlazante (repulsivo).
- De un electrón que se encuentra en el orbital
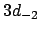 del átomo de hidrógeno
sabemos que
del átomo de hidrógeno
sabemos que
- El módulo de su momento angular orbital vale
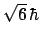 y su componente
y su componente 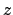 vale
vale
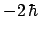 .
.
- El módulo de su momento angular orbital vale
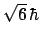 y su componente
y su componente 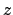 vale
vale
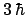 .
.
- El módulo de su momento angular orbital vale
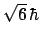 y sus componentes
y sus componentes 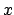 ,
, 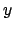 y
y 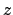 valen
valen
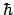 ,
, 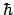 y
y 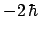 , respectivamente
, respectivamente
- El módulo de su momento angular orbital vale
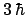 y su componente
y su componente 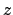 vale
vale
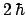 .
.
- La energía de ionización (o función de trabajo) del potasio metálico
es menor que la del niquel metálico. Indica cuál de las siguientes afirmaciones
será correcta:
- La longitud de onda crítica (o umbral) para el K es mayor que para el Ni.
- La frecuencia crítica (o umbral) del Ni es menor que para el K.
- La energía de ionización de estos metales no puede relacionarse
con sus propiedades fotoeléctricas.
- Un electrón liberado del K por luz de una cierta frecuencia tiene una
velocidad menor que un electrón liberado del Ni por luz de la misma frecuencia.
- El hamiltoniano electrónico de la molécula de HeH
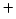 , donde los subíndices 1 y
2 denotan los electrones, es:
, donde los subíndices 1 y
2 denotan los electrones, es:
-
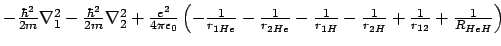
-
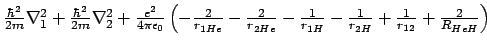
-
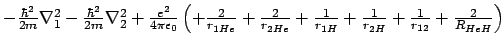
-
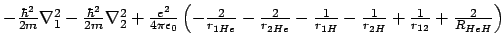
- Cuando una partícula confinada en una caja monodimensional de longitud
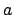 se encuentra en un estado descrito por la función de onda
se encuentra en un estado descrito por la función de onda
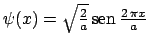 (
(
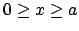 )
)
- La densidad de probabilidad de encontrarla en
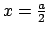 es
mayor que en
es
mayor que en
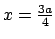 .
.
- La densidad de probabilidad de encontrarla en
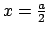 es nula.
es nula.
- La densidad de probabilidad de encontrarla en
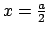 es
mayor que en
es
mayor que en
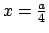 .
.
- La probablidad de encontrarla en
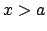 no es nula.
no es nula.
- Un átomo excitado puede volver a su estado fundamental por dos caminos distintos.
En el primero, pasa a un estado intermedio emitiendo radiación de longitud de
onda
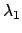 y después al fundamental emitiendo radiación de longitud de
onda
y después al fundamental emitiendo radiación de longitud de
onda 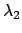 . En el segundo camino, pasa directamente al estado fundamental
emitiendo radiación de longitud de onda
. En el segundo camino, pasa directamente al estado fundamental
emitiendo radiación de longitud de onda 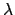 .
¿Cuál será la relación entre
.
¿Cuál será la relación entre 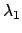 ,
, 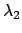 y
y 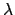 ?
?
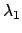 +
+ 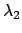 =
= 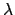
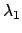 -
- 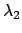 =
= 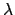
-
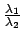 =
=
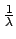
-
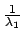 +
+
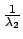 =
=
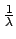
- Sea un oscilador armónico monodimensional.
- La degeneración de un determinado nivel es
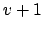 , donde
, donde
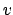 es el número cuántico vibracional.
es el número cuántico vibracional.
- La energía mínima del sistema es nula.
- La energía mínima del sistema vale
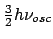 .
.
- Los niveles energéticos no están degenerados.
- ¿Cuál de las siguientes partículas es menos probable que
atraviese una barrera de potencial de 2.0 eV de altura por efecto túnel?
- Un electrón con una energía de 0.2 eV.
- Un protón con una energía de 1.0 eV.
- Un electrón con una energía de 1.0 eV.
- Un protón con una energía de 0.2 eV.
- ¿Cuál de las siguientes transiciones entre orbitales de un átomo hidrogenoide
corresponde a una transición permitida de la serie de Lyman?
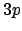
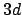
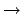
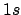
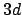
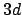
- La aproximación de Born-Oppenheimer implica que:
- la energía de los núcleos es cero.
- se puede tratar el movimiento de los electrones sin tener en cuenta la
posición de los núcleos.
- la energía potencial bajo la que se mueven los núcleos surge de
resolver la ecuación de Schrödinger electrónica.
- la velocidad de movimiento de los electrones es menor que la de los núcleos.
- Considerese la función de onda del estado fundamental del ion Li
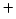 .
.
- La función de onda completa no cambia de signo al intercambiar las
coordenadas de dos electrones.
- La función de onda completa sólo depende de las coordenadas
espaciales.
- La función de onda completa debe ser simétrica al intercambiar las
coordenadas de dos electrones.
- La función de onda completa debe ser antisimétrica al intercambiar las
coordenadas de dos electrones.
- Las propiedades ondulatorias de una partícula se hacen más patentes:
- al aumentar su velocidad.
- al aumentar su momento lineal.
- al aumentar su longitud de onda de De Broglie.
- al disminuir su longitud de onda de De Broglie.
- Un átomo en un estado excitado tiene un tiempo de vida de 10 ms. La
energía del estado excitado:
- se puede medir con un error mayor que 10
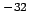 J.
J.
- se puede medir con tanta precisión como se quiera.
- no se puede medir.
- se puede medir con un error menor que 10
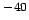 J.
J.
- Una función de onda válida para una partícula libre de masa
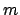 moviéndose en el eje
moviéndose en el eje 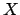 es
es
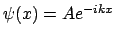 .
Esta función:
.
Esta función:
- Es autofunción del operador momento lineal (
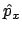 )
con autovalor 0.
)
con autovalor 0.
- Es autofunción del operador momento lineal (
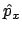 )
con autovalor
)
con autovalor 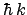 .
.
- Es autofunción del operador momento lineal (
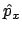 )
con autovalor
)
con autovalor 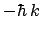 .
.
- No es autofunción del operador momento lineal (
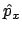 ).
).
Nota:
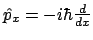 .
.
- Para una partícula de masa
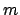 que se mueve en la dimensión X,
el operador
que se mueve en la dimensión X,
el operador 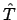 es
es
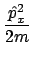 .
Para este caso, el conmutador
.
Para este caso, el conmutador
![$
\left[\hat{p}_x,\hat{T}\right]
$](img60.gif) vale
vale
- 1
- -1
- 0
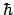
- Dada la función de onda
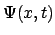 que cumple que
que cumple que
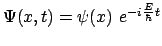 ,
podemos decir de ella que:
,
podemos decir de ella que:
- no es solución de la ecuación de Schrödinger dependiente del
tiempo.
- describe estados no estacionarios del sistema.
- la densidad de probabilidad que describe no depende del tiempo.
- describe un sistema en el cual la energía
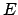 depende del tiempo.
depende del tiempo.
- Las funciones
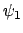 y
y 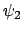 son autofunciones del operador
son autofunciones del operador
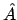 (lineal y hermítico) con autovalores
(lineal y hermítico) con autovalores 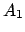 y
y 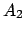 ,
respectivamente.
Una función de onda
,
respectivamente.
Una función de onda
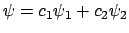 con
con 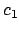 y
y 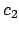 distintos de 0,
distintos de 0,
- es autofunción de
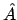 sólo si
sólo si 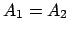 .
.
- nunca es autofunción de
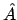 .
.
- siempre es autofunción de
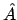 .
.
- a veces es autofunción de
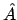 , con autovalor
, con autovalor
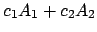 .
.
- Los niveles de energía estacionarios para el átomo de
hidrógeno, obtenidos a partir de la ec. de Schrödinger
no relativista con el hamiltoniano electrostático
- son directamente proporcionales a
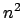 .
.
- el espaciado entre los niveles es constante.
- la energía del estado fundamental es nula.
- son inversamente proporcionales a
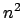 .
.
© Copyright.
UAM
2006-10-10

