Puntuación:

- Cada respuesta correcta suma 1/2 punto.
- Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
- Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya
respuesta se conozca con seguridad. Sólo hay una respuesta correcta en
cada pregunta.
En la hoja de respuestas no olvidéis rellenar:
- NOMBRE Y APELLIDOS.
- DNI.
- MODELO (Importante: toda hoja de respuestas sin modelo
equivale a un suspenso).
- Un átomo excitado puede volver a su estado fundamental por dos caminos distintos.
En el primero, pasa a un estado intermedio emitiendo radiación de frecuencia
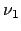 y después al fundamental emitiendo radiación de frecuencia
y después al fundamental emitiendo radiación de frecuencia
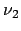 . En el segundo camino, pasa directamente al estado fundamental
emitiendo radiación de frecuencia
. En el segundo camino, pasa directamente al estado fundamental
emitiendo radiación de frecuencia 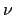 .
¿Cuál será la relación entre
.
¿Cuál será la relación entre 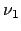 ,
, 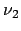 y
y 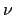 ?
?
-
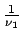 +
+
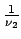 =
= 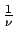
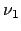 -
- 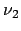 =
= 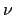
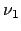 +
+ 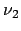 =
= 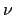
-
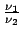 =
= 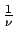
- En el efecto fotoeléctrico, la velocidad con que son expulsados los electrones
- disminuye al aumentar la longitud de onda de la radiación incidente.
- aumenta al aumentar la intensidad de la radiación incidente.
- disminuye al aumentar la frecuencia de la radiación incidente.
- aumenta al aumentar la longitud de onda de la radiación incidente.
- Las propiedades ondulatorias se hacen más patentes:
- sin depender de la masa de las partículas.
- entre dos partículas con igual velocidad, para aquella cuya masa sea mayor.
- entre dos partículas con igual masa, para aquella cuya velocidad sea menor.
- cuanto mayor sea la energía cinética de la partícula.
- Según la mecánica cuántica, dos propiedades físicas
se pueden medir simultáneamente con tanta precisión como se
desee
- nunca.
- si el conmutador de sus respectivos operadores vale 0.
- siempre.
- si el conmutador de sus respectivos operadores vale -
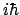 .
.
- Para una partícula de masa
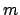 que se mueve en la dimensión X,
el conmutador
que se mueve en la dimensión X,
el conmutador
![$\left[\hat{x},\hat{p}_x\right]$](img12.gif) vale
vale
-
![$\left[\hat{p}_x,\hat{x}\right]$](img13.gif) .
.
- 0.
- -
![$\left[\hat{p}_x,\hat{x}\right]$](img13.gif) .
.
- No es posible determinar este conmutador.
- Una función de onda válida para una partícula de masa
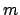 moviéndose en el eje
moviéndose en el eje 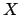 dentro de una caja de potencial
es
dentro de una caja de potencial
es
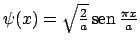 .
Esta función:
.
Esta función:
- No es autofunción del operador momento lineal (
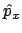 ).
).
- Es autofunción del operador momento lineal (
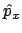 )
con autovalor
)
con autovalor 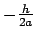 .
.
- Es autofunción del operador momento lineal (
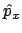 )
con autovalor 0.
)
con autovalor 0.
- Es autofunción del operador momento lineal (
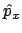 )
con autovalor
)
con autovalor 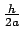 .
.
Nota:
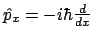 .
.
- Cuando un sistema se encuentra en un estado estacionario
descrito por la función de onda
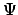
- su energía
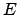 se obtiene de resolver la ecuación
se obtiene de resolver la ecuación
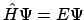 y es una función del tiempo.
y es una función del tiempo.
- su energía
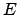 es constante y el valor de
es constante y el valor de 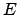 se obtiene resolviendo la
ecuación
se obtiene resolviendo la
ecuación
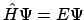 .
.
- su energía no se puede conocer.
- un sistema cuántico no se puede encontrar nunca en un estado estacionario.
- El operador mecanocuántico de energía cinética de una
partícula
tiene dimensiones de
- energía
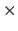 tiempo.
tiempo.
- energía / tiempo.
- energía.
- las mismas unidades que
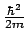 .
.
- Se tienen dos protones
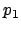 y
y 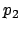 moviéndose independientemente
en una dimensión con la misma energía E. El protón
moviéndose independientemente
en una dimensión con la misma energía E. El protón 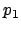 se encuentra en su camino con una barrera de potencial de altura
3E y de grosor
se encuentra en su camino con una barrera de potencial de altura
3E y de grosor 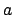 . El protón
. El protón 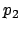 se encuentra en su camino
con una barrera de potencial de altura 5E y de grosor 2
se encuentra en su camino
con una barrera de potencial de altura 5E y de grosor 2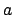 .
¿Cuál de las siguientes afirmaciones es correcta?
.
¿Cuál de las siguientes afirmaciones es correcta?
- Ambos protones tienen la misma probabilidad de atravesar la barrera.
- La probabilidad de que el protón
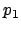 atraviese la barrera es mayor
que la del protón
atraviese la barrera es mayor
que la del protón 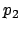 .
.
- La probabilidad de que el protón
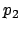 atraviese la barrera es mayor
que la del protón
atraviese la barrera es mayor
que la del protón 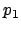 .
.
- No es posible determinar qué protón tiene más probabilidad de
atravesar la barrera porque ambos son independientes.
- Cuando un oscilador armónico monodimensional se encuentra en un estado descrito
por una función de onda
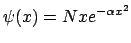
- La densidad de probabilidad de encontrarlo en
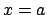 es
igual que en
es
igual que en 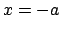 .
.
- La densidad de probabilidad de encontrarlo en
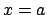 es
mayor que en
es
mayor que en 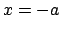 .
.
- La densidad de probabilidad de encontrarlo en
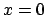 es máxima.
es máxima.
- La probablidad de encontrarlo en
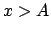 , donde A representa el punto de retorno clásico,
es nula.
, donde A representa el punto de retorno clásico,
es nula.
- En una caja tridimensional con las tres dimensiones iguales (
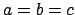 ),
),
- no siempre que dos números cuánticos sean iguales existe degeneración.
- existe degeneración siempre que dos números cuánticos sean iguales.
- no existe degeneración en sus niveles de energía.
- la máxima degeneración es tres.
- Para un rotor rígido que se encuentra en un estado
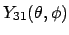 (o para un
átomo de hidrógeno cuya parte angular sea
(o para un
átomo de hidrógeno cuya parte angular sea
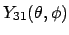 )
)
- el módulo de su momento angular orbital vale
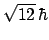 y su componente
y su componente 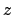 vale
vale
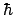 .
.
- el módulo de su momento angular orbital vale
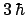 y su componente
y su componente 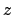 vale
vale
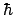 .
.
- el módulo de su momento angular orbital vale
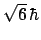 y su componente
y su componente 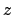 vale
vale
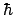 .
.
- el módulo de su momento angular orbital vale
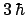 y su componente
y su componente 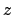 vale
vale
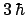 .
.
- Los números cuánticos correspondientes al siguiente orbital de un átomo hidrogenoide
son:
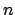 = 3,
= 3, 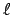 = 2,
= 2, 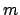 = -1
= -1
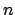 = 3,
= 3, 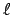 = 1,
= 1, 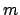 = 0
= 0
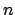 = 3,
= 3, 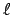 = 2,
= 2, 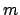 = 1
= 1
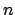 = 2,
= 2, 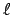 = 3,
= 3, 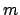 = -1
= -1
- ¿Cuál de las siguientes funciones puede usarse para representar correctamente
un estado del ion Li
 ?
?
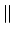
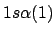
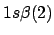
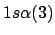
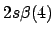
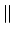
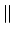
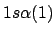
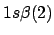
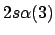
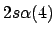
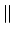
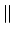
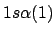
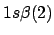
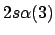
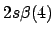
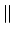
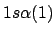
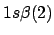
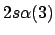
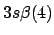
Nota: La nomenclatura
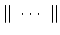 representa un determinante de Slater formado a partir
de los spin-orbitales reseñados.
representa un determinante de Slater formado a partir
de los spin-orbitales reseñados.
- ¿Cuál de las siguientes funciones de dos electrones no cumple el principio
de exclusión de Pauli?
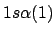
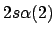 -
- 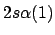
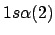
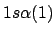
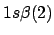 -
- 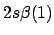
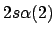
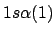
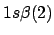 -
- 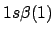
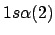
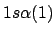
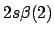 -
- 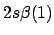
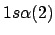
- Considerese un átomo polielectrónico, ¿cuál de las siguientes afirmaciones
es falsa?
- El número de términos espectrales proveniente de una configuración electrónica
dada puede ser mayor que uno.
- Una vez dada la configuración electrónica, puedo saber el número de términos
espectrales a los
que da lugar y ordenarlos energéticamente.
- Puedo tener un mismo término espectral para configuraciones electrónicas
distintas.
- Sólo se puede tener un término espectral para cada configuración electrónica.
- El término espectral fundamental para el átomo de Si
([Ne], 3
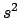 3
3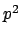 ) es:
) es:
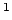 P
P
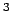 F
F
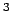 P
P
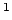 D
D
- El hamiltoniano electrónico de la molécula de HeH
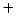 , donde los subíndices 1 y
2 denotan los electrones, es:
, donde los subíndices 1 y
2 denotan los electrones, es:
-
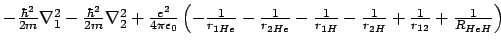
-
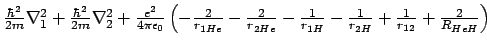
-
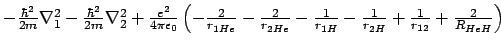
-
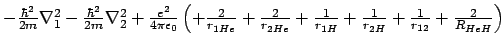
- ¿Cuál de las siguientes afirmaciones es cierta?
- La aproximación de Born-Oppenheimer sólo se puede emplear
para moléculas diatómicas.
- La aproximación de Born-Oppenheimer se basa en que las velocidades de los
electrones son mucho menores que las de los núcleos.
- La aproximación de Born-Oppenheimer se basa en que las velocidades de los
electrones de los núcleos son muy similares.
- La aproximación de Born-Oppenheimer se basa en que las velocidades de los
electrones son mucho mayores que las de los núcleos.
- La función de onda
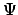 del estado fundamental del H
del estado fundamental del H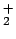 ,
,
- describe una menor densidad electrónica entre los núcleos
que el caso de dos átomos separados.
- describe una mayor densidad electrónica entre los núcleos
que el caso de dos átomos separados.
- describe la misma densidad electrónica entre los núcleos
que el caso de dos átomos separados.
- posee un plano nodal, perpendicular al eje internuclear,
entre los núcleos.
© Copyright.
Alfredo Aguado
2005-10-13

