Puntuación:

- Cada respuesta correcta suma 1/2 punto.
- Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
- Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya
respuesta se conozca con seguridad. Sólo hay una respuesta correcta en
cada pregunta.
En la hoja de respuestas no olvidéis rellenar:
- el nombre y apellidos.
- el DNI.
- el MODELO (Importante: toda hoja de respuestas sin modelo
equivale a un suspenso).
- La interpretación del efecto fotoeléctrico
ha sido posible tras aceptar:
- que la radiación electromagnética también tiene una naturaleza corpuscular
- que la materia también tiene una naturaleza ondulatoria
- el principio de indeterminación
- que la energía de la materia está cuantizada
- Las longitud de onda de De Broglie asociado a un protón
- es menor que la asociada a un electrón con la misma velocidad
- es igual que la asociada a un electrón con la misma velocidad
- es mayor que la asociada a un electrón con la misma velocidad
- no existe; sólo se puede asociar una longitud de onda a los fotones
- Se desea medir simultáneamente la posición,
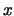 , y el momento lineal,
, y el momento lineal,
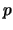 , de un electrón con una precisión
, de un electrón con una precisión 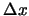 y
y 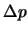 ,
respectivamente.
Sabiendo que
,
respectivamente.
Sabiendo que
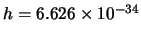 J s:
J s:
- se pueden medir si
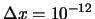 m y
m y
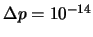 kg m s
kg m s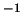
- se pueden medir si
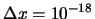 m y
m y
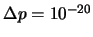 kg m s
kg m s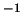
- se pueden medir ambas magnitudes simultáneamente
con tanta precisión como se desee
- no se pueden medir ambas magnitudes en ningún caso
- En un estado estacionario de un sistema:
- la energía no cambia con el tiempo
- la energía varía periódicamente con el tiempo
- la energía crece exponencialmente con el tiempo
- la energía decrece exponencialmente con el tiempo
- La existencia de degeneración sistemática en los niveles de energía
de un sistema:
- es consecuencia de la existencia de simetría en el sistema
- es consecuencia de la energía del punto cero
- es consecuencia del principio de indeterminación de Heisenberg
- es consecuencia de las transiciones entre dos o más niveles de energía
- El operador mecanocuántico de energía cinética de una partícula,
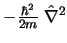 :
:
- tiene dimensiones de energía
- tiene dimensiones de energía
 tiempo
tiempo
- tiene dimensiones de energía
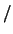 tiempo
tiempo
- es adimensional
- En el caso de una partícula en una caja monodimensional limitada
por
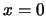 y
y 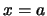 que se encuentra en el estado estacionario
que se encuentra en el estado estacionario 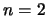 ,
su densidad de probabilidad:
,
su densidad de probabilidad:
- es nula en el centro de la caja y máxima en
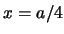 y
y 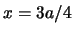
- es nula en el centro de la caja, en
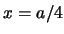 y en
y en 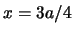
- es máxima en el centro de la caja
- es la misma en cualquier punto de la caja.
- El número de nodos de las funciones de onda de los estados
estacionarios de una partícula en una caja monodimensional
- es 0 en el estado fundamental y aumenta de uno en uno al pasar a estados
excitados
- es 1 en el estado fundamental y aumenta de uno en uno al pasar a estados
excitados
- es máximo en el estado fundamental y disminuye de uno en uno al pasar
a estados excitados
- es independiente del valor de su número cuántico
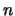
- En un oscilador armónico tridimensional isótropo
[
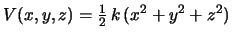 ]
de masa
]
de masa 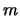 y frecuencia de vibración clásica
y frecuencia de vibración clásica
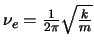 ,
el primer estado excitado es
,
el primer estado excitado es
- triplemente degenerado, con una energía de
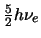
- triplemente degenerado, con una energía de
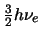
- no degenerado, con una energía de
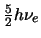
- no degenerado, con una energía de
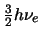
- El primer estado excitado de un oscilador armónico monodimensional
- tiene una densidad de probabilidad nula en
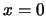
- tiene una densidad de probabilidad máxima en
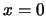
- tiene una función de onda que toma el mismo valor en
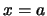 y en
y en 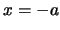
- tiene una función de onda que se anula para todo
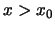 ,
siendo
,
siendo 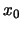 el punto de retroceso clásico
el punto de retroceso clásico
- Dada una cierta barrera de energía potencial de 2 eV,
¿cuál de las siguientes partículas tiene una mayor probabilidad de
atravesarla por el efecto túnel?
- un electrón con una energía de 1.9 eV
- un electrón con una energía de 0.1 eV
- un protón con una energía de 1.9 eV
- un protón con una energía de 0.1 eV
- Dado un rotor rígido de masa reducida
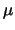 y distancia
y distancia 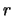 ,
la dependencia del ángulo
,
la dependencia del ángulo 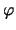 y la energía total
de un estado de números cuánticos
y la energía total
de un estado de números cuánticos 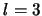 (ó
(ó 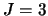 ) y
) y 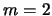 son:
son:
-
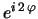 y
y
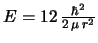 , respectivamente
, respectivamente
-
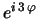 y
y
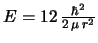 , respectivamente
, respectivamente
-
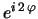 y
y
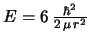 , respectivamente
, respectivamente
-
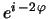 y
y
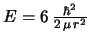 , respectivamente
, respectivamente
- De un electrón que se encuentra en el orbital
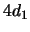 del átomo de
hidrógeno se sabe que el módulo y la componente
del átomo de
hidrógeno se sabe que el módulo y la componente 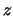 de su momento angular
valen:
de su momento angular
valen:
-
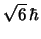 y
y 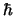 , respectivamente
, respectivamente
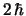 y
y 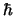 , respectivamente
, respectivamente
-
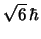 y
y 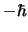 , respectivamente
, respectivamente
-
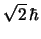 y
y 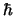 , respectivamente
, respectivamente
- Los números cuánticos del orbital del átomo de hidrógeno
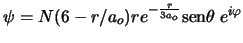 son:
son:
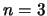 ,
, 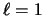 ,
, 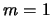 .
.
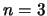 ,
, 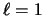 ,
, 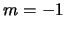 .
.
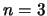 ,
, 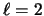 ,
, 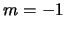 .
.
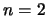 ,
, 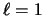 ,
, 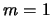 .
.
- El valor medio de la distancia electrón-núcleo en un estado
de un átomo hidrogenoide descrito por el orbital normalizado
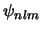 es:
es:
-
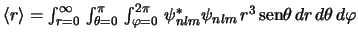
-
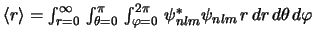
-
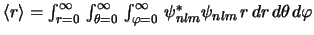
-
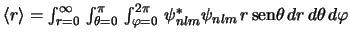
- Un determinante de Slater se puede utilizar como
función de onda aproximada de un estado de un átomo multielectrónico
porque es una función que:
- cambia de signo cuando se intercambian dos electrones
- no cambia de signo cuando se intercambian dos electrones
- es la solución exacta de la ecuación de Schrödinger si se elige adecuadamente
- no tiene en cuenta el espín de los electrones
- El término espectral fundamental del átomo de C es
(si se desprecia el acoplamiento espín-órbita)
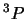
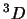
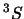
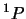
- Cuando se usa la función de onda del modelo de electrones
independientes,
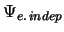 , para describir el estado fundamental
del átomo de He,
el valor medio de la energía con el hamiltoniano exacto, que es
, para describir el estado fundamental
del átomo de He,
el valor medio de la energía con el hamiltoniano exacto, que es
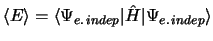 si la función está normalizada,
si la función está normalizada,
- es mayor que el valor exacto de la energía del estado fundamental
- es menor que el valor exacto de la energía del estado fundamental
- concide con el valor exacto de la energía del estado fundamental
- es igual a la energía del ion He
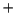
- El Hamiltoniano del ion Be
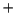 , donde
los subíndices 1, 2 y 3 se refieren a los electrones, es:
, donde
los subíndices 1, 2 y 3 se refieren a los electrones, es:
-
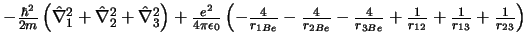
-
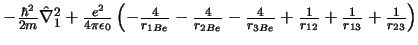
-
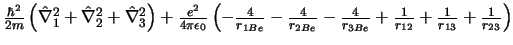
-
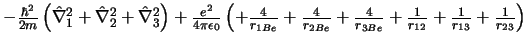
- En una molécula diatómica,
el primer paso de la aproximación de Born-Oppenheimer consiste en la
solución de la ecuación
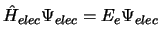 ,
con
,
con
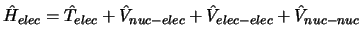 ,
a cada valor de la distancia internuclear.
,
a cada valor de la distancia internuclear.
- La distancia de enlace es aquella en la que
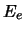 toma el valor más bajo
toma el valor más bajo
- La distancia de enlace es aquella en la que
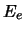 toma el valor más alto
toma el valor más alto
- La distancia de enlace es aquella en la que dicha ecuación tiene
solución exacta
- El cálculo de la distancia de enlace requiere resolver el segundo paso
de la aproximación de Born-Oppenheimer
© Copyright. Noemí Fernández. Noviembre 2003

