Puntuación:

- Cada respuesta correcta suma 1/2 punto.
- Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
- Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya
respuesta se conozca con seguridad. Sólo hay una respuesta correcta en
cada pregunta.
En la hoja de respuestas no olvidéis rellenar:
- el nombre y apellidos.
- el DNI.
- el MODELO (Importante: toda hoja de respuestas sin modelo
equivale a un suspenso).
- La difracción de electrones es una manifestación de:
- La naturaleza corpuscular de la materia.
- La naturaleza ondulatoria de la radiación.
- La naturaleza corpuscular de la radiación.
- La naturaleza ondulatoria de la materia.
- Un electrón que se mueve con un momento lineal de módulo
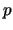 tiene
una onda asociada cuya longitud de onda
tiene
una onda asociada cuya longitud de onda 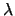 :
:
- Es
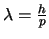 pero no puede medirse en un experimento de difracción.
pero no puede medirse en un experimento de difracción.
- Es
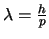 y puede medirse en un experimento de difracción.
y puede medirse en un experimento de difracción.
- Es
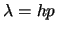 y puede medirse en un experimento de difracción.
y puede medirse en un experimento de difracción.
- Un electrón no tiene una onda asociada.
- Según el principio de indeterminación de Heisenberg:
- La posición y el momento lineal de una partícula no pueden conocerse
simultáneamente con total precisión, salvo en casos excepcionales.
- La posición de una partícula nunca puede conocerse con total
precisión.
- La posición y el momento lineal de una partícula nunca pueden conocerse
simultáneamente con total precisión.
- El momento lineal de una partícula nunca puede conocerse con total
precisión.
- En Mecánica Cuántica,
la evolución en el tiempo del estado de un sistema se obtiene:
- Resolviendo la ecuación de Schrödinger independiente del tiempo.
- Resolviendo la ecuación de autovalores para el momento angular.
- Resolviendo la ecuación de Schrödinger dependiente del tiempo.
- No se puede obtener.
- Una función de onda que sea aceptable para describir un estado cualquiera
de un sistema:
- Es necesario que sea monovaluada (o unívoca) y continua.
- Puede tomar dos valores en el mismo punto.
- Debe ser independiente del tiempo.
- Es suficiente que sea compleja y monovaluada (o unívoca).
- El operador Hamiltoniano,
 , de una partícula que se
mueve a lo largo del eje
, de una partícula que se
mueve a lo largo del eje 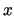 se obtiene:
se obtiene:
- Escribiendo la fórmula de la energía clásica en función de
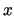 y de
y de 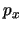 y substituyendo
y substituyendo 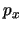 por el operador
por el operador
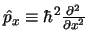
- Escribiendo la fórmula de la energía clásica en función de
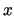 y de
y de 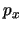 y
derivando con respecto a
y
derivando con respecto a 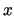 .
.
- Escribiendo la fórmula de la energía clásica en función de
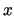 y de
y de 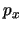 y substituyendo
y substituyendo 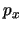 por el operador
por el operador
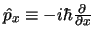
- Por deducción, a partir del principio de indeterminación
de Heisenberg.
- El valor medio o esperado de la energía:
- Es una magnitud que se puede obtener directamente en una sola medida.
- Representa la media de los valores obtenidos al hacer varias medidas
de la energía.
- Representa la media de los valores obtenidos al hacer varias medidas
del cuadrado de la energía.
- Es siempre nulo, independientemente del cero de energía elegido.
- La ecuación de Schrödinger independiente del tiempo de una
caja monodimensional limitada por
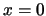 y
y 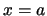 es:
es:
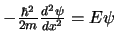 .
Las funciones de onda
.
Las funciones de onda
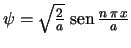 ,
con
,
con 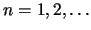 :
:
- Son las únicas soluciones de esa ecuación diferencial que cumplen
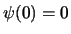 y
y 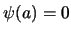 y no están normalizadas.
y no están normalizadas.
- Son las únicas soluciones de esa ecuación diferencial,
estén o no normalizadas.
- No son solución de esa ecuación diferencial, pero se aceptan porque están
cuantizadas.
- Son las únicas soluciones de esa ecuación diferencial que cumplen
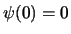 ,
, 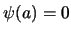 y están normalizadas.
y están normalizadas.
- En una caja de tres dimensiones en la que
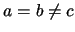 :
:
- Los estados (1,2,1) y (2,1,1) están degenerados.
- Los estados (1,2,1) y (1,1,2) están degenerados.
- Los tres estados (2,1,1), (1,2,1) y (1,1,2) están degenerados.
- Los tres estados (2,1,1), (1,2,1) y (1,1,2) tienen distinta energía.
- En un oscilador armónico monodimensional, las frecuencias
del espectro de absorción
correspondientes a las transiciones entre niveles energéticos
consecutivos (v
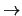 v+1):
v+1):
- Aumentan al aumentar el número cuántico v.
- Disminuyen al aumentar el número cuántico v.
- Son inversamente proporcionales a la energía de los niveles.
- Son todas iguales
- La probabilidad de que una partícula de masa
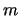 con energía cinética
con energía cinética 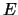 atraviese una barrera de potencial de altura
atraviese una barrera de potencial de altura 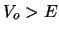 y
anchura
y
anchura 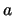 por efecto túnel:
por efecto túnel:
- Aumenta si aumentamos la altura de la barrera.
- Es menor para un protón que para un electrón.
- Es independiente de la energía de la partícula.
- Aumenta si aumentamos la anchura de la barrera.
- Un nivel de energía de un rotor rígido
de masa reducida
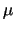 y distancia
y distancia 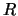 vale:
vale:
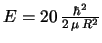 .
.
- Se trata del nivel de número cuántico J=4 [o
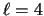 ] y contiene 1 estado.
] y contiene 1 estado.
- Se trata del nivel de número cuántico J=4 [o
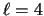 ] y contiene 9 estados degenerados.
] y contiene 9 estados degenerados.
- Se trata del nivel de número cuántico J=20 [o
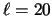 ] y contiene 1 estado.
] y contiene 1 estado.
- Se trata del nivel de número cuántico J=20 [o
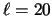 ] y contiene 20 estados degenerados.
] y contiene 20 estados degenerados.
- De un electrón que se encuentra en el orbital
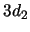 del átomo de
hidrógeno sabemos que:
del átomo de
hidrógeno sabemos que:
- El módulo de su momento angular vale
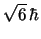 y su componente
y su componente 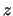 vale
vale 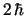 .
.
- El módulo de su momento angular vale
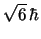 y sus componentes
y sus componentes 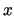 ,
, 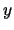 ,
, 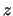 valen respectivamente
0, 0 y
valen respectivamente
0, 0 y 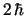 .
.
- El módulo de su momento angular vale
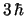 y su componente
y su componente 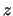 vale
vale 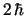 .
.
- El módulo de su momento angular vale
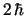 y su componente
y su componente 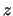 vale
vale 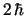 .
.
- Para un electrón en el átomo de hidrógeno en un estado descrito
por la función de onda
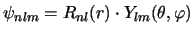 [o
[o
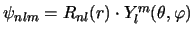 ],
la densidad de probabilidad en el punto
],
la densidad de probabilidad en el punto
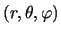 es
proporcional a:
es
proporcional a:
-
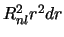
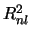
-
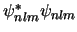
-
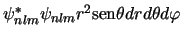
- Los números cuánticos del orbital del átomo de hidrógeno
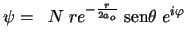 son:
son:
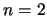 ,
, 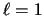 ,
, 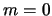 .
.
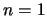 ,
, 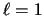 ,
, 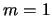 .
.
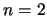 ,
, 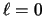 ,
, 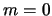 .
.
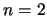 ,
, 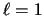 ,
, 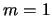 .
.
- El término más estable de la configuración excitada
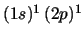 del Li
del Li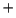 es:
es:
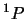 .
.
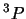 .
.
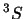 .
.
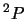 .
.
- ¿Cuál de las siguientes funciones de dos electrones
no cumple el principio de exclusión de Pauli?
-
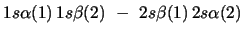
-

-

-
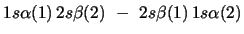
- Se calcula la energía del estado fundamental del átomo de He
por medio de
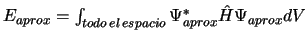 ,
en donde
,
en donde
![$\Psi_{aprox} = \frac{1}{\sqrt{2}}
[ 1s\alpha(1)\,1s\beta(2)\,\,-\,\,1s\beta(1)\,1s\alpha(2) ]$](img61.gif) ,
siendo
,
siendo
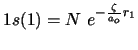 y
y
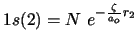 .
Si el valor exacto de dicha energía es
.
Si el valor exacto de dicha energía es 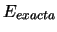 :
:
-
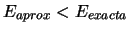 sea cual sea el valor que se tome de
sea cual sea el valor que se tome de 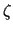 .
.
-
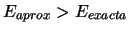 sea cual sea el valor que se tome de
sea cual sea el valor que se tome de 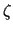 .
.
-
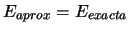 si se toma
si se toma 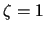 .
.
-
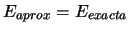 si se toma
si se toma 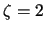 .
.
- En la aproximación de Born-Oppenheimer,
la curva de energía potencial nuclear
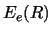 se obtiene:
se obtiene:
- Resolviendo
![$[ \hat{T}_{nuc} + \hat{V}_{nuc-elec}
+ \hat{V}_{nuc-nuc} ] \Psi_{nuc} = E_{e} \Psi_{nuc}$](img72.gif) a cada valor de la distancia internuclear R.
a cada valor de la distancia internuclear R.
- Resolviendo
![$[ \hat{T}_{elec}
+ \hat{V}_{elec-elec} ] \Psi_{e} = E_{e} \Psi_{e}$](img73.gif) a cada valor de la distancia internuclear R.
a cada valor de la distancia internuclear R.
- Resolviendo
![$[ \hat{T}_{elec} + \hat{V}_{nuc-elec}
+ \hat{V}_{elec-elec} + \hat{V}_{nuc-nuc} ] \Psi_{e} = E_{e} \Psi_{e}$](img74.gif) a cada valor de la distancia internuclear R.
a cada valor de la distancia internuclear R.
- Resolviendo
![$[ \hat{T}_{elec} + \hat{V}_{nuc-elec}
+ \hat{V}_{elec-elec} + \hat{V}_{nuc-nuc} ] \Psi_{Tot} = E_{e}
\Psi_{Tot}$](img75.gif) para un único valor de la distancia internuclear R.
para un único valor de la distancia internuclear R.
- La configuración electrónica más estable de la molécula F
 y su orden de enlace son:
y su orden de enlace son:
-
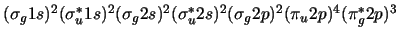 ,
con orden de enlace 1.5.
,
con orden de enlace 1.5.
-
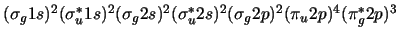 ,
con orden de enlace 1.
,
con orden de enlace 1.
-
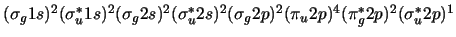 ,
con orden de enlace 1.5
,
con orden de enlace 1.5
-
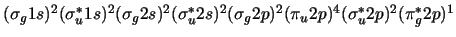 ,
con orden de enlace 1.5
,
con orden de enlace 1.5
© Copyright.
Noemí Fernández
2003-02-28


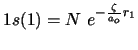 y
y
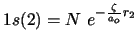 .
Si el valor exacto de dicha energía es
.
Si el valor exacto de dicha energía es