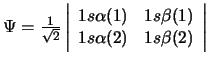Examen de Fundamentos de Química Cuántica (Septiembre 2001)
 1
1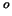 de C. Químicas.
de C. Químicas.
Puntuación: 
- Cada respuesta correcta suma 1/2 punto.
- Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
- Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya
respuesta se conozca con seguridad. Sólo hay una respuesta correcta en
cada pregunta.
En la hoja de respuestas no olvidéis rellenar:
- el nombre y apellidos.
- el DNI.
- el MODELO (Importante: toda hoja de respuestas sin modelo
equivale a un suspenso).
- La longitud
 de la onda asociada a un electrón
de masa
de la onda asociada a un electrón
de masa 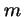 acelerado hasta la velocidad
acelerado hasta la velocidad 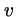 (
(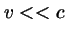 ):
):
- Es
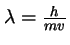 , pero no puede medirse.
, pero no puede medirse.
- Es
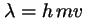 y puede medirse en un experimento de difracción.
y puede medirse en un experimento de difracción.
- Es
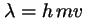 , pero no puede medirse.
, pero no puede medirse.
- Es
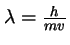 y puede medirse en un experimento de difracción.
y puede medirse en un experimento de difracción.
- El operador Hamiltoniano,
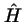 , de una partícula que se
mueve a lo largo del eje
, de una partícula que se
mueve a lo largo del eje 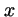 se obtiene:
se obtiene:
- Escribiendo la fórmula de la energía clásica en función de
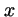 y de
y de 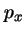 y substituyendo después
y substituyendo después 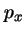 por el operador
por el operador

- Escribiendo la fórmula de la energía clásica en función de
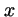 y de
y de 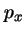 y substituyendo después
y substituyendo después 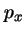 por el operador
por el operador
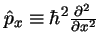
- Escribiendo la fórmula de la energía clásica en función de
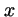 y de
y de 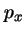 y
derivando con respecto a
y
derivando con respecto a 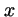 .
.
- Por deducción, a partir del principio de indeterminación
de Heisenberg.
- Cuando un sistema está en un estado cualquiera,
tanto si es estacionario como si no,
su función de onda
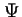 cumple:
cumple:
-
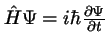
-
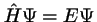 .
.
-
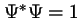 .
.
- Se elige arbitrariamente y no tiene que cumplir ninguna ecuación.
- Cuando una partícula está en un estado
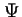 estacionario,
la densidad de probabilidad de encontrar a la partícula:
estacionario,
la densidad de probabilidad de encontrar a la partícula:
- Depende de la posición de la misma y del tiempo.
- No depende de la posición de la misma pero sí del tiempo.
- Depende de la posición de la misma pero no del tiempo.
- No depende de la posición de la misma ni del tiempo.
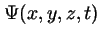 es la función de onda de una partícula en un
estado dado.
La probabilidad de encontrar a dicha partícula en un volumen
diferencial
es la función de onda de una partícula en un
estado dado.
La probabilidad de encontrar a dicha partícula en un volumen
diferencial 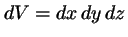 en torno al punto
en torno al punto 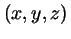 en el
instante
en el
instante 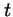 :
:
- Es
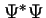 si
si 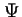 está normalizada a la unidad.
está normalizada a la unidad.
- Es
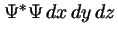 si
si 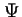 está normalizada a la unidad.
está normalizada a la unidad.
- Es
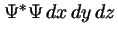 .
.
- Es
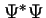 .
.
- En el caso de una partícula en una caja monodimensional
de longitud
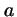 , en el que
, en el que
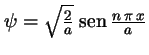 ,
se puede decir que:
,
se puede decir que:
- La densidad de probabilidad del estado
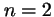 es máxima en el centro de
la caja.
es máxima en el centro de
la caja.
- La densidad de probabilidad es máxima en el centro de la caja para todos
los estados.
- La densidad de probabilidad del estado
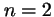 es nula en el centro de
la caja.
es nula en el centro de
la caja.
- La densidad de probabilidad es nula en el centro de la caja para todos
los estados.
- En el sistema formado por una partícula en una caja
existen estados degenerados en energía:
- Para cualquier caja de dimensión mayor o igual que 2
- Sólo si la caja es tridimensional.
- Para cualquier caja, sea monodimensional, bidimensional, tridimensional,
...
- Para cualquier caja de dimensión mayor o igual que 2 y con dos
o más lados iguales.
- Los niveles de energía de un oscilador armónico monodimensional
vienen dados por:
-
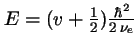 , con
, con
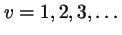 ,
en donde
,
en donde
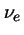 es la frecuencia de vibración clásica
(o frecuencia fundamental de vibración).
es la frecuencia de vibración clásica
(o frecuencia fundamental de vibración).
-
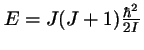 , con
, con
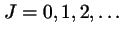 ,
en donde
,
en donde 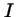 es su momento de inercia.
es su momento de inercia.
-
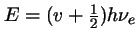 , con
, con
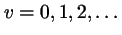 ,
en donde
,
en donde
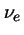 es la frecuencia de vibración clásica
(o frecuencia fundamental de vibración).
es la frecuencia de vibración clásica
(o frecuencia fundamental de vibración).
-
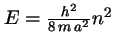 , con
, con
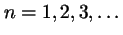 ,
en donde
,
en donde 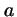 es la distancia de equilibrio del oscilador.
es la distancia de equilibrio del oscilador.
- En el oscilador armónico monodimensional la probabilidad de
encontrar valores de
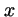 no comprendidos entre los puntos
de retorno clásico:
no comprendidos entre los puntos
de retorno clásico:
- Es negativa.
- No es nula.
- Es nula ya que la energía cinética es menor que cero.
- Es nula ya que la energía potencial es menor que cero.
- El efecto túnel:
- Tendrá más importancia en las reacciones de transferencia
de protones que en las de transferencia de electrones.
- Tendrá más importancia en las reacciones de transferencia
de electrones que en las de transferencia de protones.
- Afectará en la misma medida a las reacciones de transferencia
de protones que a las de transferencia de electrones.
- No tendrá ninguna influencia en las reacciones de transferencia
de protones ni en las de transferencia de electrones.
- Para una partícula que se comporta como un rotor rígido
en tres dimensiones:
- La energía y el cuadrado del momento angular
no se pueden conocer con exactitud simultáneamente.
- La energía mínima del sistema no puede ser 0.
- La energía es la única cantidad que aparece cuantizada
y no puede tomar nunca el valor 0.
- La energía y el cuadrado del momento angular
aparecen cuantizados y pueden valer 0.
- La componente
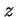 del momento angular de un electrón en el átomo de
hidrógeno cuando está en el orbital
del momento angular de un electrón en el átomo de
hidrógeno cuando está en el orbital 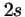 y cuando está en el
y cuando está en el 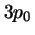 :
:
- Vale cero en ambos casos.
- Vale cero en el primer caso y
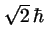 en el segundo.
en el segundo.
- Vale
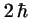 en el primer caso y
en el primer caso y 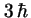 en el segundo.
en el segundo.
- No se puede saber cuánto vale en ninguno de los dos casos.
- Indica cuál de las siguientes afirmaciones es cierta para la
función de onda de un átomo de hidrogenoide:
-
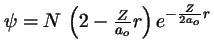 corresponde a
corresponde a 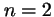 ,
, 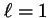 ,
, 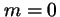
-
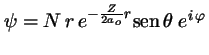 corresponde a
corresponde a 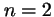 ,
, 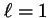 ,
, 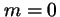
-
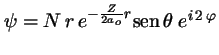 corresponde a
corresponde a 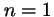 ,
, 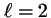 ,
, 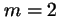 .
.
-
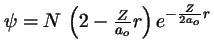 corresponde a
corresponde a 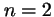 ,
, 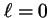 ,
, 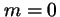
- En un átomo hidrogenoide, un estado caracterizado por
los números cuánticos
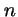 ,
, 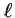 y
y 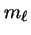 :
:
- Tiene valores perfectamente definidos de E,
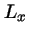 ,
, 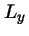 ,
, 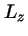 .
.
- Tiene valores perfectamente definidos de E,
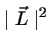 ,
, 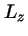 .
.
- Tiene valores perfectamente definidos de E,
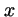 ,
, 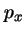 .
.
- Sólo la energía está perfectamente definida.
- Para un electrón
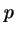 del átomo de hidrógeno,
la función radial:
del átomo de hidrógeno,
la función radial:
- Tiene un número decreciente de nodos en la serie
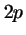 ,
, 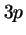 ,
, 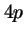 , ....
, ....
- Tiene el mismo número de nodos en el orbital
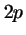 que en el
que en el 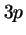 .
.
- Tiene un número creciente de nodos en la serie
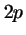 ,
, 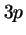 ,
, 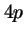 , ....
, ....
- No tiene nodos para ningún valor de
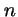 .
.
- La configuración excitada
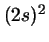 del átomo de He
da lugar a:
del átomo de He
da lugar a:
- Un término
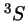 con degeneración 3.
con degeneración 3.
- Cuatro estados agrupados en dos niveles o términos espectrales:
uno triplemente degenerado,
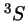 , y otro no degenerado,
, y otro no degenerado, 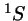 .
.
- Un término
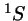 con un solo estado no degenerado.
con un solo estado no degenerado.
- Cuatro estados con cuatro energías diferentes.
- Cuál de las siguientes funciones es antisimétrica respecto
al intercambio de electrones?
-
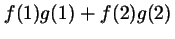
-
![$[f(1)-f(2)] [g(1)g(2)]$](img67.gif)
-
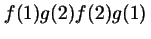
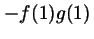
- Para el átomo de He, la función
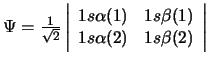
- Es una función aproximada del estado fundamental del He
en la aproximación orbital.
- Es la única función de onda válida para cualquier estado del He.
- Es una solución exacta de la ecuación de Schrödinger
independiente del tiempo,
- Se anula, ya que hay dos filas iguales.
- En la aproximación de Born-Oppenheimer
se considera:
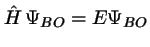 ,
con
,
con
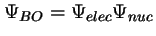 y
y
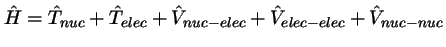 .
.
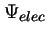 se obtiene fijando las posiciones de los núcleos
y resolviendo
se obtiene fijando las posiciones de los núcleos
y resolviendo
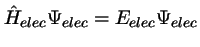 ,
con
,
con
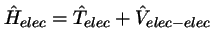
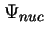 se obtiene fijando las posiciones de los electrones
y resolviendo
se obtiene fijando las posiciones de los electrones
y resolviendo
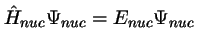 ,
con
,
con
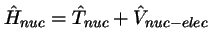
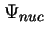 se obtiene fijando las posiciones de los electrones
y resolviendo
se obtiene fijando las posiciones de los electrones
y resolviendo
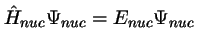 ,
con
,
con
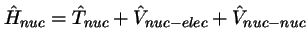
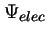 se obtiene fijando las posiciones de los núcleos
y resolviendo
se obtiene fijando las posiciones de los núcleos
y resolviendo
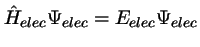 ,
con
,
con
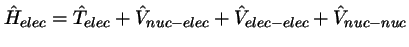 .
.
- La función de onda más simple de la Teoría de Orbitales
Moleculares para el estado fundamental de la molécula
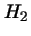 es:
es:
-
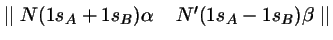
-
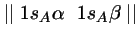
-
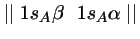
-
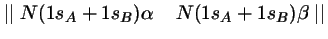
© Copyright.
Cristina Sanz Sanz
2002-04-02
![]()
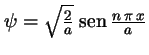 ,
se puede decir que:
,
se puede decir que:
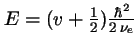 , con
, con
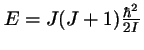 , con
, con
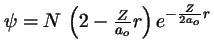 corresponde a
corresponde a 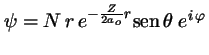 corresponde a
corresponde a 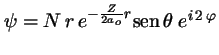 corresponde a
corresponde a 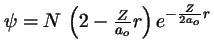 corresponde a
corresponde a