Examen de Fundamentos de Química Cuántica (96/97)

- Cada respuesta correcta suma 1/2 punto.
- Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
- Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya
respuesta se conozca con seguridad. Sólo hay una respuesta correcta en
cada pregunta.
En la hoja de respuestas no olvidéis rellenar:
- el nombre y apellidos.
- el DNI.
- el MODELO (Importante: toda hoja de respuestas sin modelo
equivale a un suspenso).
- Un átomo excitado puede volver al estado fundamental de dos maneras.
En la primera, pasa a un estado intermedio emitiendo radiación de longitud de onda
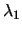 , y después al estado fundamental emitiendo radiación de longitud de onda
, y después al estado fundamental emitiendo radiación de longitud de onda
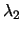 .
En la segunda pasa directamente al estado fundamental emitiendo radiación de longitud
de onda
.
En la segunda pasa directamente al estado fundamental emitiendo radiación de longitud
de onda 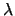 . ¿Cuál será la relación entre
. ¿Cuál será la relación entre
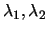 y
y 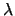 ?
?
-
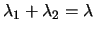
-
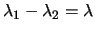
-
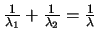
-
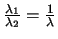
- La energía de ionización del Cesio metálico es menor que la correspondiente al
Wolframio. Indica cuál de las siguientes afirmaciones será correcta:
- La longitud de onda crítica (o umbral) para el Cesio es mayor que para el Wolframio.
- La frecuencia crítica (o umbral) del Wolframio es menor que la del Cesio.
- La energía de ionización de estos metales no puede relacionarse con sus
propiedades fotoeléctricas.
- Un electrón liberado del Cesio por luz de una cierta frecuencia, tiene una
velocidad menor que un electrón liberado del Wolframio por luz de la misma frecuencia.
- La degeneración de los niveles de energía de un sistema es consecuencia de:
- Las transiciones entre dos o más niveles de energía.
- Una gran diferencia de energía entre dos o más niveles.
- La simetría del sistema.
- La energía del punto cero.
- La longitud de onda de De Broglie de una partícula libre:
- Es independiente de la energía cinética.
- Es independiente de la velocidad.
- Es directamente proporcional a la velocidad.
- Es inversamente proporcional a su masa.
- Una función de onda aproximada y aceptable para el estado electrónico
fundamental del Li
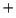 viene dada por:
viene dada por:
-
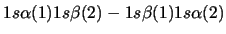
-
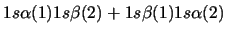
-
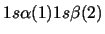
-
![$1s(1) 1s(2) [\alpha(1) - \beta(2)]$](img16.gif)
- Una partícula está sometida al potencial
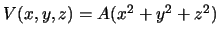 donde
donde 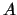 es una constante positiva.
es una constante positiva.
- Las energías de los estados estacionarios de esa partícula pueden expresarse
somo la suma de tres energías, cada una proporcional a
 y
y 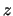 , respectivamente.
, respectivamente.
- Entre las energías de los estados estacionarios de esa partícula no aparece
degeneración.
- Las funciones de onda de los estados estacionarios de esa partícula pueden
expresarse como productos de tres funciones, que dependen de
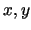 y
y 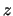 respectivamente.
respectivamente.
- La energía del estado fundamental es igual a la del mínimo del potencial.
- La función de onda del primer estado excitado de una partícula en una
caja monodimensional de longitud
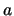 , con paredes de potencial infinitas, es
, con paredes de potencial infinitas, es
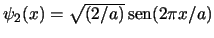 para
para 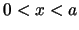 .
Cuando la partícula se encuentra en dicho estado:
.
Cuando la partícula se encuentra en dicho estado:
- La probabilidad de encontrarla en
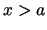 no es nula.
no es nula.
- La densidad de probabilidad en
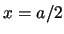 es nula.
es nula.
- La densidad de probabilidad en
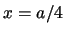 es mayor que en
es mayor que en 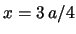 .
.
- La densidad de probabilidad en
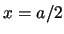 es mayor que en
es mayor que en 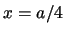 .
.
- El Hamiltoniano electrónico de la molécula HeH
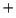 , donde los subíndices
1 y 2 se refieren a los electrones, es:
, donde los subíndices
1 y 2 se refieren a los electrones, es:
-
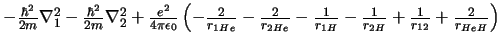
-
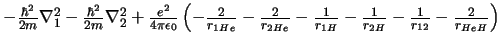
-
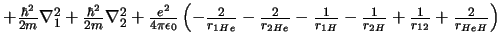
-
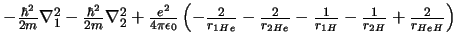
- La densidad de probabilidad de una partícula en un estado estacionario:
- Depende del tiempo.
- Es independiente de las coordenadas espaciales de la partícula.
- Es independiente del tiempo.
- Depende de las coordenadas espaciales y del tiempo.
- Para una molécula diatómica heteronuclear
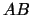 , donde el eje
, donde el eje  es el
eje internuclear, decir cuál de las siguientes afirmaciones es correcta:
es el
eje internuclear, decir cuál de las siguientes afirmaciones es correcta:
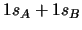 es un orbital
es un orbital 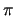 .
.
-
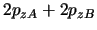 es un orbital
es un orbital 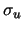 .
.
-
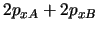 es un orbital
es un orbital 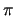 .
.
-
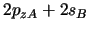 es un orbital
es un orbital 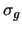 .
.
- En el oscilador armónico monodimensional:
- Hay estados degenerados entre los estados excitados.
- Si doblamos la masa de la partícula la energía de los estados estacionarios
disminuye a la mitad.
- El estado fundamental posee una energía distinta de la del mínimo del potencial.
- La energía puede tomar cualquier valor.
- Considere la función de onda del estado fundamental del átomo de Helio:
- La función de onda cambia de signo al intercambiar las coordenadas de dos
electrones.
- Dicha función es exactamente el producto de dos orbitales
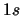 .
.
- La parte espacial de dicha función debe ser antisimétrica al intercambiar las
coordenadas de dos electrones.
- Debido al principio de incertidumbre, el helio no tiene estado
fundamental.
- Cuál de las siguientes afirmaciones es cierta:
- En la aproximación de Born-Oppenheimer no tiene sentido dibujar curvas de potencial
para los estados electrónicos de moléculas diatómicas.
- La aproximación de Born-Oppenheimer se basa en que las velocidades de electrones
y núcleos son muy similares.
- La aproximación de Born-Oppenheimer sólo se puede emplear para moléculas
diatómicas.
- La aproximación de Born-Oppenheimer se basa en la gran diferencia de masas entre
electrones y núcleos.
- Los orbitales moleculares de la molécula de H
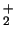 cumplen:
cumplen:
- Son soluciones de la ecuación de Schrödinger nuclear.
- No tiene sentido clasificarlos como
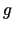 o
o 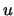 .
.
- Son soluciones de la ecuación de Schrödinger electrónica.
- Su energía es independiente de la distancia internuclear.
- En la configuración electrónica del estado fundamental de una molécula
diatómica, AB, el orbital ocupado de mayor energía es antienlazante:
- Esta molécula tiene energía de disociación inferior a la del ion positivo AB
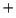 .
.
- Esta molécula es necesariamente inestable.
- Esta molécula tiene energía de disociación superior a la del ion positivo AB
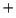 .
.
- No es posible encontrar orbitales antienlazantes en moléculas heteronucleares.
- La densidad electrónica en el punto medio del eje internuclear,
de los orbitales moleculares
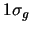 y
y 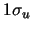 de la molécula de H
de la molécula de H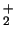 :
:
- Es mayor, para ambos, que la de los orbitales atómicos
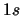
- Es menor, para ambos, que la de los orbitales atómicos
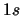
- Es menor para el
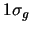 que la de los dos orbitales atómicos
que la de los dos orbitales atómicos 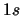 y es
mayor para el
y es
mayor para el 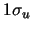 .
.
- Es mayor para el
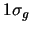 que la de los dos orbitales atómicos
que la de los dos orbitales atómicos 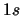 y es
menor para el
y es
menor para el 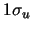 .
.
- En átomos polielectrónicos las energías orbitales son:
- Función de los números cuánticos
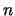 y
y 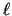 .
.
- Función sólo del número cuántico principal
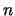 .
.
- Directamente proporcionales al número cuántico
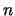 .
.
- Directamente proporcionales al número cuántico
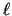 .
.
- Cuáles de las siguientes transiciones del espectro electrónico de un átomo
hidrogenoide corresponden a transiciones permitidas de la serie de Balmer:
-
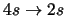
-
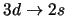
-
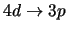
-
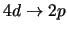
- El orbital hidrogenoide
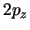
- Es una función que crece exponencialmente con
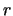 .
.
- Tiene una función de distribución radial que presenta dos máximos.
- Tiene un único nodo radial.
- No presenta nodos en su parte radial.
- Considerar la transición
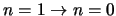 del espectro vibracional de
las moléculas FH y FD, que se suponen osciladores armónicos con la misma constante de fuerza.
del espectro vibracional de
las moléculas FH y FD, que se suponen osciladores armónicos con la misma constante de fuerza.
- La frecuencia de la transición del FD es el doble de la frecuencia del FH.
- La longitud de onda de la transición FD es el doble de la longitud de onda
del FH.
- La longitud de onda de la transición es distinta para ambas moléculas.
- La frecuencia de la transición es la misma para ambas moléculas.
© Copyright.
Cristina Sanz Sanz
2002-04-02
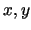 y
y 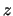 , respectivamente.
, respectivamente.
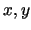 y
y 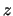 respectivamente.
respectivamente.
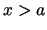 no es nula.
no es nula.
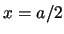 es nula.
es nula.
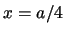 es mayor que en
es mayor que en 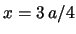 .
.
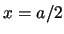 es mayor que en
es mayor que en 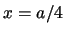 .
.
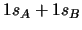 es un orbital
es un orbital 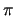 .
.
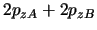 es un orbital
es un orbital 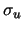 .
.
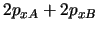 es un orbital
es un orbital 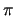 .
.
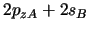 es un orbital
es un orbital 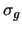 .
.
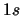 .
.
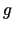 o
o 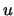 .
.
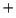 .
.
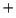 .
.
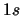
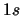
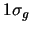 que la de los dos orbitales atómicos
que la de los dos orbitales atómicos 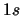 y es
mayor para el
y es
mayor para el 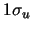 .
.
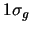 que la de los dos orbitales atómicos
que la de los dos orbitales atómicos 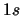 y es
menor para el
y es
menor para el 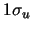 .
.
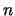 y
y 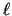 .
.
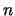 .
.
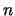 .
.
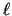 .
.
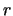 .
.
