Exámen Teórico de Fundamentos de Química Cuántica. (23 de Junio de 2008)
Puntuación:
Cada respuesta correcta suma 1/2 punto.
Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya respuesta se conozca con seguridad.
Sólo hay una respuesta correcta en cada pregunta.
- Según la interpretación de Einstein del efecto fotoeléctrico:
- la intensidad de la luz es proporcional al número de fotones.
- la intensidad de la luz es proporcional a la longitud de onda de la radiación.
- a mayor intensidad de la luz, los electrones son emitidos con mayor velocidad.
- a mayor intensidad de la luz, los electrones son emitidos con menor velocidad.
- Las propiedades ondulatorias de una partícula se hacen más patentes
- al aumentar su energía cinética.
- al aumentar su velocidad.
- al disminuir su momento lineal.
- al disminuir su longitud de onda de De Broglie.
- La interpretación de los experimentos de radiación de cuerpo negro ha sido posible tras aceptar:
- Que la energía de la materia está cuantizada.
- El principio de indeterminación.
- El dualismo onda-corpúsculo.
- Que la energía de la radiación electromagnética está cuantizada.
- La función de onda para el primer estado excitado de un oscilador armónico monodimensional es de la forma
- La densidad de probabilidad de encontrar a la partícula es nula en
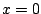 .
.
- La densidad de probabilidad de encontrar a la partícula es máxima en
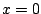 .
.
- La función tiene un mínimo en
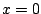 .
.
- La función toma el mismo valor en los puntos
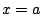 y
y 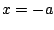 .
.
- La densidad de probabilidad de una partícula en un estado estacionario:
- Depende del tiempo.
- Es independiente de las coordenadas espaciales de la partícula.
- Es independiente del tiempo.
- Depende de las coordenadas espaciales y del tiempo.
- La función de onda
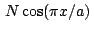 para una partícula en una caja monodimensional de longitud
para una partícula en una caja monodimensional de longitud 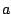 :
:
- es aceptable si los límites de la caja son
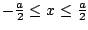 .
.
- es aceptable si los límites de la caja son
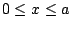 .
.
- es aceptable si los límites de la caja son
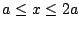 .
.
- no es aceptable en ningún caso.
- Si
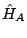 y
y 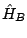 son dos hamiltonianos independientes, tales que
son dos hamiltonianos independientes, tales que
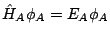 y
y
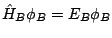 , y
, y
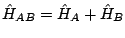 ,
cuya ecuación de valores propios es
,
cuya ecuación de valores propios es
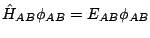 , se cumple que:
, se cumple que:
-
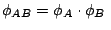 y
y
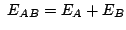 .
.
-
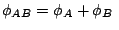 y
y
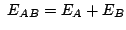 .
.
-
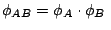 y
y
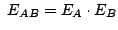 .
.
-
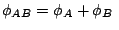 y
y
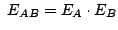 .
.
- Los niveles de energía de un oscilador armónico monodimensional vienen dados por:
-
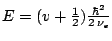 , con
, con
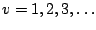 ,
en donde
,
en donde 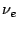 es la frecuencia de vibración clásica (o frecuencia fundamental de vibración).
es la frecuencia de vibración clásica (o frecuencia fundamental de vibración).
-
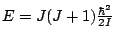 , con
, con
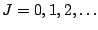 , en donde
, en donde 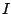 es su momento de inercia.
es su momento de inercia.
-
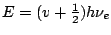 , con
, con
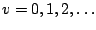 , en donde
, en donde 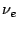 es la frecuencia de vibración clásica (o frecuencia fundamental de vibración).
es la frecuencia de vibración clásica (o frecuencia fundamental de vibración).
-
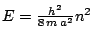 , con
, con
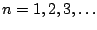 , en donde
, en donde 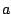 es
la distancia de equilibrio del oscilador.
es
la distancia de equilibrio del oscilador.
- Una función de onda que sea aceptable para describir un estado cualquiera de un sistema
- Debe ser independiente del tiempo.
- Puede tomar dos valores distintos en algún punto.
- Es necesario que sea monoevaluada y contínua.
- Es suficiente con que sea compleja y contínua.
- Un determinante de Slater se puede utilizar como función de onda aproximada de un estado de un átomo
multielectrónico porque es una función que:
- cambia de signo cuando se intercambian dos electrones.
- no cambia de signo cuando se intercambian dos electrones.
- permite diferenciar o discernir un electrón del otro.
- no tiene en cuenta el espín de los electrones.
- Los números cuánticos del orbital del átomo de hidrógeno
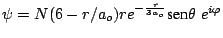 son:
son:
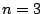 ,
, 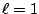 ,
, 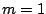 .
.
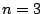 ,
, 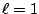 ,
, 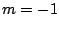 .
.
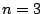 ,
, 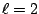 ,
, 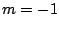 .
.
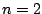 ,
, 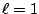 ,
, 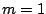 .
.
- Una función de onda aproximada y aceptable para el estado electrónico fundamental del Li
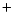 viene dada por:
viene dada por:
-
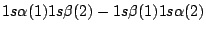
-
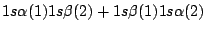
-
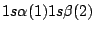
-
![$1s(1) 1s(2) [\alpha(1) - \beta(2)]$](img41.png)
- El Hamiltoniano del ion Be
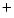 , donde los subíndices 1, 2 y 3 se refieren a los electrones, es:
, donde los subíndices 1, 2 y 3 se refieren a los electrones, es:
-
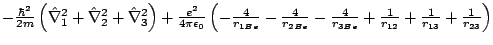
-
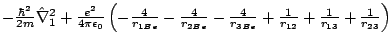
-
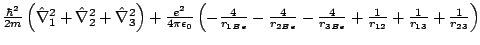
-
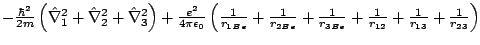
- El término más estable de la configuración excitada
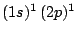 del Li
del Li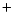 es:
es:
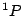 .
.
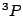 .
.
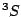 .
.
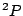 .
.
- Un electrón en un átomo hidrogenoide en un estado enlazado descrito por la
función de onda
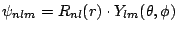 tiene una densidad
de probabilidad radial (función de distribución radial) proporcional a:
tiene una densidad
de probabilidad radial (función de distribución radial) proporcional a:
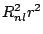
-
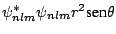
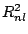
-
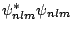
- La energía de disociación (
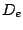 ) de la molécula de H
) de la molécula de H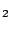 es:
es:
- La suma de la energía de los dos átomos separados y la energía del mínimo de la curva de energía potencial.
- La diferencia entre la energía de los dos átomos separados y la energía del mínimo de la curva de
energía potencial.
- La suma de la energía del punto cero y la energía del mínimo de la curva de energía potencial.
- La diferencia entre la energía del punto cero y la energía del mínimo de la curva de energía potencial.
- Para una molécula diatómica heteronuclear, donde el eje
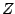 es el eje internuclear, y
es el eje internuclear, y 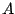 y
y 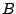 denotan los núcleos, decir cuál de las siguientes afirmaciones es correcta:
denotan los núcleos, decir cuál de las siguientes afirmaciones es correcta:
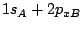 es un orbital
es un orbital 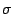 .
.
-
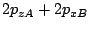 es un orbital
es un orbital 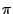 .
.
-
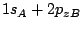 es un orbital
es un orbital 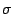 .
.
-
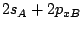 es un orbital
es un orbital 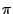 .
.
- El Hamiltoniano electrónico de la molécula LiH
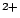 , donde los subíndices 1 y 2 se refieren a los electrones, es:
, donde los subíndices 1 y 2 se refieren a los electrones, es:
-
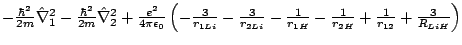
-
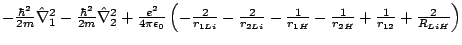
-
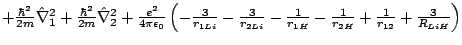
-
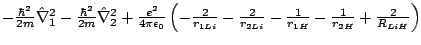
- La curva de energía electrónica frente a R (distancia internuclear) obtenida usando la aproximación de
Bohr-Oppenheimer para una molécula diatómica A-B
- nunca puede tener un mínimo para un estado electrónico excitado.
- presenta un mínimo para el estado fundamental si la molécula es estable.
- presenta un máximo a la distancia de equilibrio para el estado fundamental.
- presenta un mínimo cuando el estado es antienlazante (repulsivo).
- En la aproximación de Born-Oppenheimer se considera:
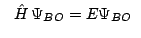 donde tenemos
donde tenemos
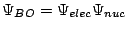 .
.
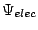 se obtiene fijando las posiciones de los núcleos y resolviendo
se obtiene fijando las posiciones de los núcleos y resolviendo
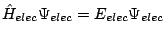 , con
, con
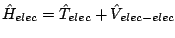
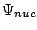 se obtiene fijando las posiciones de los electrones y resolviendo
se obtiene fijando las posiciones de los electrones y resolviendo
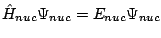 , con
, con
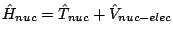
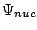 se obtiene fijando las posiciones de los electrones y resolviendo
se obtiene fijando las posiciones de los electrones y resolviendo
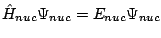 , con
, con
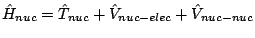
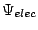 se obtiene fijando las posiciones de los núcleos y resolviendo
se obtiene fijando las posiciones de los núcleos y resolviendo
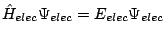 , con
, con
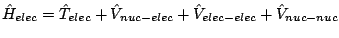 .
.
© Copyright.
Universidad Autónoma de Madrid, Departamento de Química Física Aplicada
18-08-2008
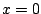 .
.
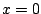 .
.
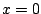 .
.
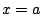 y
y 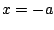 .
.
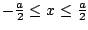 .
.
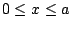 .
.
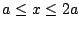 .
.
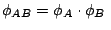 y
y
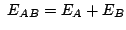 .
.
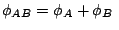 y
y
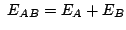 .
.
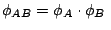 y
y
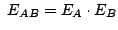 .
.
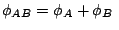 y
y
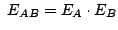 .
.
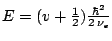 , con
, con
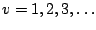 ,
en donde
,
en donde 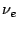 es la frecuencia de vibración clásica (o frecuencia fundamental de vibración).
es la frecuencia de vibración clásica (o frecuencia fundamental de vibración).
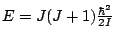 , con
, con
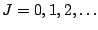 , en donde
, en donde 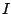 es su momento de inercia.
es su momento de inercia.
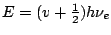 , con
, con
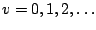 , en donde
, en donde 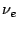 es la frecuencia de vibración clásica (o frecuencia fundamental de vibración).
es la frecuencia de vibración clásica (o frecuencia fundamental de vibración).
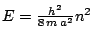 , con
, con
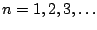 , en donde
, en donde 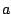 es
la distancia de equilibrio del oscilador.
es
la distancia de equilibrio del oscilador.
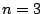 ,
, 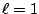 ,
, 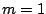 .
.
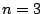 ,
, 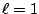 ,
, 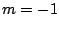 .
.
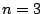 ,
, 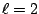 ,
, 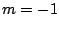 .
.
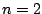 ,
, 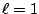 ,
, 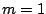 .
.
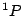 .
.
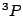 .
.
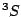 .
.
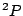 .
.
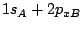 es un orbital
es un orbital 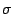 .
.
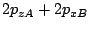 es un orbital
es un orbital 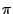 .
.
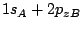 es un orbital
es un orbital 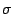 .
.
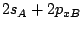 es un orbital
es un orbital 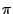 .
.
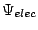 se obtiene fijando las posiciones de los núcleos y resolviendo
se obtiene fijando las posiciones de los núcleos y resolviendo
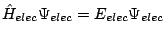 , con
, con
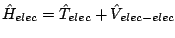
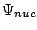 se obtiene fijando las posiciones de los electrones y resolviendo
se obtiene fijando las posiciones de los electrones y resolviendo
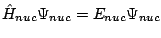 , con
, con
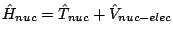
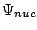 se obtiene fijando las posiciones de los electrones y resolviendo
se obtiene fijando las posiciones de los electrones y resolviendo
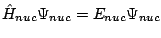 , con
, con
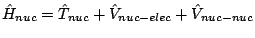
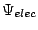 se obtiene fijando las posiciones de los núcleos y resolviendo
se obtiene fijando las posiciones de los núcleos y resolviendo
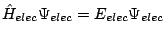 , con
, con
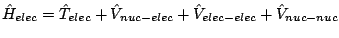 .
.