Exámen Teórico de Fundamentos de Química Cuántica. (15 de Junio de 2007)
Puntuación:
Cada respuesta correcta suma 1/2 punto.
Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya respuesta se conozca con seguridad.
Sólo hay una respuesta correcta en cada pregunta.
- La función trabajo de un metal vale 2.5 eV. Se puede extraer un electrón mediante
el efecto fotoeléctrico si se hace incidir sobre el metal:
- Un fotón de energía 1.8 eV.
- Dos fotones de energía 1.8 eV cada uno.
- Un número suficientemente grande de fotones, independientemente de su energía.
- Un fotón de energía 2.6 eV.
- Las longitud de onda de de Broglie asociado a un electrón
- es menor que la asociada a un protón con la misma velocidad.
- es igual que la asociada a un protón con la misma velocidad.
- es mayor que la asociada a un protón con la misma velocidad.
- es independiente de la velocidad.
- El efecto fotoeléctrico y la difracción de electrones son manifestaciones:
- de la naturaleza ondulatoria de la radiación electromagnética y la naturaleza
corpuscular de la materia, respectivamente,
- de la naturaleza corpuscular de la radiación electromagnética y la naturaleza
ondulatoria de la materia, respectivamente,
- de la naturaleza esencialmente diferente de la materia y de la radiación electromagnética,
- de que la energía de la radiación electromagnética es proporcional al cuadrado de la amplitud.
- Un átomo excitado puede volver al estado fundamental de dos maneras.
En la primera, pasa a un estado intermedio emitiendo radiación de longitud de onda
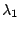 ,
y después al estado fundamental emitiendo radiación de longitud de onda
,
y después al estado fundamental emitiendo radiación de longitud de onda 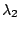 .
En la segunda pasa directamente al estado fundamental emitiendo radiación de longitud de onda
.
En la segunda pasa directamente al estado fundamental emitiendo radiación de longitud de onda 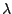 .
¿Cuál será la relación entre
.
¿Cuál será la relación entre
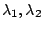 y
y 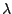 ?
?
-
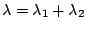
-
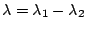
-
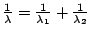
-
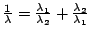
- La densidad de probabilidad para un estado estacionario, descrito por una función de onda
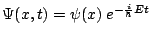 :
:
- Aumenta exponencialmente con el tiempo,
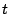 .
.
- Disminuye exponencialmente con el tiempo,
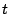 .
.
- Es independiente de la posición,
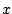 .
.
- Es independiente del tiempo,
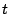 .
.
- Se desea medir simultáneamente la posición,
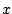 , y el momento lineal,
, y el momento lineal, 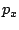 , de una partícula
con una precisión
, de una partícula
con una precisión 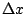 y
y 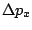 respectivamente.
Sabiendo que
respectivamente.
Sabiendo que 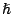 = 1.055
= 1.055 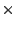 10
10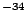 J
J s,
s,
- Ambas magnitudes se pueden medir simultáneamente con tanta precisión como se desee.
- No es posible, en ningún caso, medir las dos variables simultáneamente.
- Es posible obtener una medida con
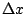 = 10
= 10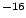 m y
m y 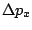 = 10
= 10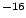 kg m/s
kg m/s
- Es posible obtener una medida con
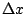 = 10
= 10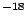 m y
m y 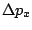 = 10
= 10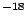 kg m/s
kg m/s
- Para una partícula de masa
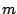 que se mueve en la dimensión
que se mueve en la dimensión 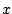 , el operador
, el operador 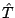 es
es
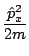 . Para este caso, el conmutador
. Para este caso, el conmutador
![$ \left[\hat{T},\hat{p}_x\right] $](img24.png) vale
vale
- 1
- -1
- 0
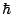
Nota:
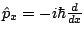
- En Mecánica Cuántica, a cada propiedad observable corresponde un operador, cuya expresión:
- Se obtiene a partir su expresión en mecánica clásica en función de
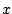 ,
, 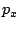 , ...,
aplicando la ecuación de Schrödinger.
, ...,
aplicando la ecuación de Schrödinger.
- Sólo existe para
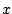 y
y 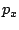 , con
, con
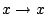 ,
,
 .
.
- Se obtiene a partir de su expresión en mecánica clásica en función de
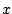 ,
, 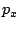 , ...,
sustituyendo
, ...,
sustituyendo
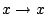 ,
,
 , ...
, ...
- Se postula independientemente para cada observable.
- En una caja bidimensional de lados
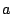 y
y 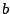 , los estados (
, los estados (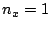 ,
, 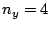 ) y (
) y (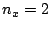 ,
, 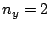 )
están degenerados si:
)
están degenerados si:
 .
.
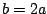 .
.
-
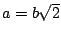 .
.
-
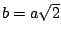 .
.
- Sea
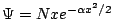 una función de onda válida para un oscilador armónico monodimensional.
una función de onda válida para un oscilador armónico monodimensional.
- La función de onda es mínima para
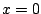 .
.
- La función densidad de probabilidad se anula para
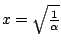 .
.
- La función densidad de probabilidad es mínima para
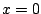 .
.
- La función de onda tiene el mismo valor para
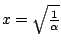 que para
que para
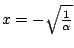
- La energía de un átomo hidrogenoide en un estado descrito por los números cuánticos
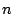 ,
, 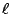 y
y 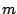 :
:
- Es proporcional a
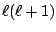 .
.
- Es proporcional a
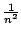 .
.
- Es proporcional a
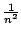 y a
y a 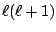 .
.
- Depende de
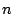 ,
, 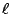 y
y 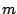 .
.
- El modulo del momento angular de un electrón en el átomo de hidrógeno
cuando está en el orbital
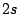 y cuando está en el
y cuando está en el 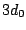 :
:
- Vale cero en ambos casos.
- Vale
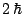 en el primer caso y
en el primer caso y 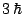 en el segundo.
en el segundo.
- Vale cero en el primer caso y
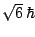 en el segundo.
en el segundo.
- No se puede saber cuánto vale en ninguno de los dos casos.
- Los números cuánticos del orbital del átomo de hidrógeno
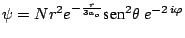 son:
son:
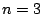 ,
, 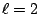 ,
, 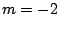 .
.
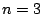 ,
, 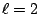 ,
, 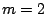 .
.
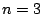 ,
, 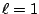 ,
, 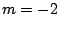 .
.
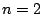 ,
, 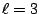 ,
, 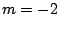 .
.
- ¿Cuál de las siguientes funciones es antisimétrica respecto al intercambio de electrones?
-
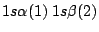 .
.
-
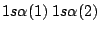 .
.
-
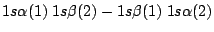 .
.
-
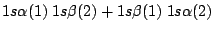 .
.
- La configuración excitada
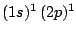 del átomo de He da lugar a:
del átomo de He da lugar a:
- Un término espectral más estable,
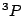 , y otro menos estable
, y otro menos estable 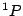 .
.
- Un solo término espectral
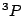 .
.
- Un solo término espectral
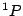 .
.
- Un estado no degenerado
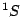 .
.
- El Hamiltoniano electrónico de la molécula LiH
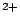 , donde los subíndices 1 y 2 se refieren a los electrones, es:
, donde los subíndices 1 y 2 se refieren a los electrones, es:
-
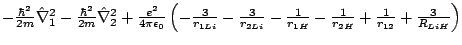
-
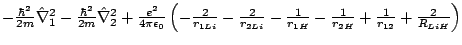
-
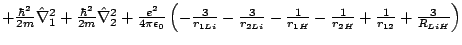
-
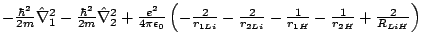
- La configuración electrónica del estado fundamental de la molécula diatómica B
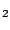 es
es
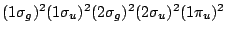 . Teniendo en cuenta el orden de enlace, decir cuál de las siguientes afirmaciones es correcta:
. Teniendo en cuenta el orden de enlace, decir cuál de las siguientes afirmaciones es correcta:
- El ion positivo B
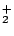 tiene una energía de disociación mayor que la de la molécula neutra B
tiene una energía de disociación mayor que la de la molécula neutra B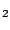 .
.
- El ion positivo B
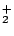 tiene una energía de disociación menor que la de la molécula neutra B
tiene una energía de disociación menor que la de la molécula neutra B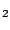 .
.
- El ion negativo B
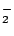 tiene una energía de disociación menor que la de la molécula neutra B
tiene una energía de disociación menor que la de la molécula neutra B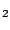 .
.
- Esta molécula es necesariamente inestable.
- En la aproximación de Born-Oppenheimer, la curva de energía potencial nuclear
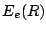 se obtiene:
se obtiene:
- Resolviendo
![$[ \hat{T}_{nuc} + \hat{V}_{nuc-elec} + \hat{V}_{nuc-nuc} ] \Psi_{nuc} = E_{e} \Psi_{nuc}$](img79.png) a cada valor de la distancia internuclear R.
a cada valor de la distancia internuclear R.
- Resolviendo
![$[ \hat{T}_{elec} + \hat{V}_{elec-elec} ] \Psi_{e} = E_{e} \Psi_{e}$](img80.png) a cada valor de la distancia internuclear R.
a cada valor de la distancia internuclear R.
- Resolviendo
![$[ \hat{T}_{elec} + \hat{V}_{nuc-elec} + \hat{V}_{elec-elec} + \hat{V}_{nuc-nuc} ] \Psi_{e} = E_{e} \Psi_{e}$](img81.png) a cada valor de la distancia internuclear R.
a cada valor de la distancia internuclear R.
- Resolviendo
![$[ \hat{T}_{elec} + \hat{V}_{nuc-elec} + \hat{V}_{elec-elec} + \hat{V}_{nuc-nuc} ] \Psi_{Tot} = E_{e} \Psi_{Tot}$](img82.png) para un único valor de la distancia internuclear R.
para un único valor de la distancia internuclear R.
- En una molécula diatómica homonuclear...
- todos los orbitales g son siempre enlazantes y todos los u son antienlazantes.
- los orbitales
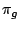 son enlazantes y los
son enlazantes y los 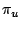 son antienlazantes.
son antienlazantes.
- los orbitales
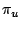 son enlazantes y los
son enlazantes y los 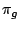 son antienlazantes.
son antienlazantes.
- no tiene sentido hablar de orbitales g y u.
- Una configuración electrónica de la molécula
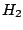 es
es
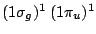 .
El término espectral de menor energía compatible con esta configuración es:
.
El término espectral de menor energía compatible con esta configuración es:
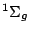
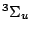
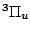
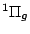
© Copyright.
Universidad Autónoma de Madrid, Departamento de Química Física Aplicada
18-08-2008
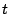 .
.
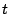 .
.
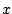 .
.
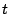 .
.
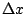 = 10
= 10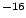 m y
m y 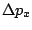 = 10
= 10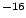 kg m/s
kg m/s
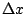 = 10
= 10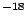 m y
m y 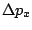 = 10
= 10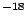 kg m/s
kg m/s
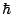
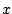 ,
, 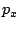 , ...,
aplicando la ecuación de Schrödinger.
, ...,
aplicando la ecuación de Schrödinger.
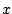 y
y 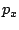 , con
, con
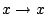 ,
,
 .
.
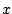 ,
, 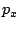 , ...,
sustituyendo
, ...,
sustituyendo
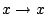 ,
,
 , ...
, ...
 .
.
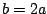 .
.
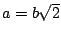 .
.
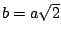 .
.
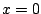 .
.
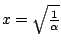 .
.
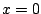 .
.
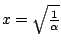 que para
que para
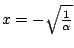
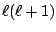 .
.
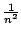 .
.
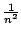 y a
y a 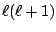 .
.
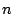 ,
, 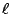 y
y 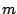 .
.
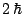 en el primer caso y
en el primer caso y 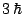 en el segundo.
en el segundo.
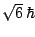 en el segundo.
en el segundo.
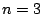 ,
, 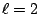 ,
, 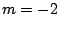 .
.
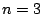 ,
, 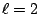 ,
, 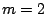 .
.
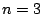 ,
, 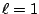 ,
, 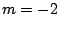 .
.
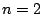 ,
, 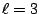 ,
, 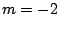 .
.
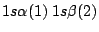 .
.
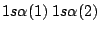 .
.
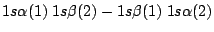 .
.
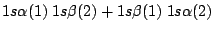 .
.
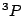 , y otro menos estable
, y otro menos estable 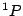 .
.
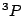 .
.
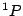 .
.
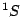 .
.
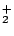 tiene una energía de disociación mayor que la de la molécula neutra B
tiene una energía de disociación mayor que la de la molécula neutra B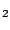 .
.
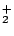 tiene una energía de disociación menor que la de la molécula neutra B
tiene una energía de disociación menor que la de la molécula neutra B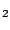 .
.
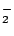 tiene una energía de disociación menor que la de la molécula neutra B
tiene una energía de disociación menor que la de la molécula neutra B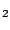 .
.
![$[ \hat{T}_{nuc} + \hat{V}_{nuc-elec} + \hat{V}_{nuc-nuc} ] \Psi_{nuc} = E_{e} \Psi_{nuc}$](img79.png) a cada valor de la distancia internuclear R.
a cada valor de la distancia internuclear R.
![$[ \hat{T}_{elec} + \hat{V}_{elec-elec} ] \Psi_{e} = E_{e} \Psi_{e}$](img80.png) a cada valor de la distancia internuclear R.
a cada valor de la distancia internuclear R.
![$[ \hat{T}_{elec} + \hat{V}_{nuc-elec} + \hat{V}_{elec-elec} + \hat{V}_{nuc-nuc} ] \Psi_{e} = E_{e} \Psi_{e}$](img81.png) a cada valor de la distancia internuclear R.
a cada valor de la distancia internuclear R.
![$[ \hat{T}_{elec} + \hat{V}_{nuc-elec} + \hat{V}_{elec-elec} + \hat{V}_{nuc-nuc} ] \Psi_{Tot} = E_{e} \Psi_{Tot}$](img82.png) para un único valor de la distancia internuclear R.
para un único valor de la distancia internuclear R.
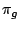 son enlazantes y los
son enlazantes y los 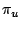 son antienlazantes.
son antienlazantes.
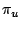 son enlazantes y los
son enlazantes y los 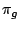 son antienlazantes.
son antienlazantes.