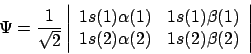Puntuación:

- Cada respuesta correcta suma 1/2 punto.
- Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
- Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya
respuesta se conozca con seguridad. Sólo hay una respuesta correcta en
cada pregunta.
En la hoja de respuestas no olvidéis rellenar:
- NOMBRE Y APELLIDOS.
- DNI.
- MODELO (Importante: toda hoja de respuestas sin modelo
equivale a un suspenso).
- La función de onda
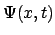 de un estado estacionario,
solución de la ecuación de Schrödinger dependiente del tiempo,
se puede factorizar como el producto de una función espacial por otra que depende del tiempo
de la forma
de un estado estacionario,
solución de la ecuación de Schrödinger dependiente del tiempo,
se puede factorizar como el producto de una función espacial por otra que depende del tiempo
de la forma
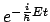 .
La densidad de probabilidad para este estado:
.
La densidad de probabilidad para este estado:
- Aumenta exponencialmente con el tiempo.
- Disminuye exponencialmente con el tiempo.
- Es independiente de
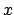 .
.
- Es independiente del tiempo.
- La función de onda que describe a una partícula confinada por un potencial
tiene que ser:
- Monovaluada, continua y de cuadrado integrable.
- Solamente monovaluada y continua.
- Solamente monovaluada y de cuadrado integrable.
- Bivaluada.
- El conmutador entre los operadores mecanocuánticos de
momento lineal (
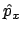 ) y de posición (
) y de posición (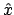 ),
),
![$\left[ \hat{p}_x, \hat{x} \right]$](img8.gif) :
:
- Vale
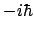
- Vale
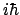
- Vale
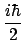
- No tiene un valor preciso, el principio de incertidumbre de Heisenberg lo impide.
- La probabilidad de que una partícula con energía cinética
dada (
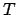 ) atraviese por efecto túnel una barrera de energía potencial
) atraviese por efecto túnel una barrera de energía potencial
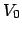 , tal que
, tal que 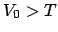 y de anchura
y de anchura 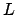 :
:
- Es nula.
- Aumenta al aumentar la altura de la barrera
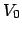 .
.
- Aumenta al aumentar la anchura de la barrera
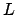 .
.
- Aumenta al disminuir la masa de la partícula.
- ¿Cuál de las siguientes afirmaciones es cierta?
- La posición y el momento lineal de una partícula pueden conocerse con total precisión
en determinadas circunstancias si se dispone del instrumental experimental adecuado.
- La posición o el momento lineal de una partícula nunca se pueden medir.
- La naturaleza ondulatoria de la materia conduce a imprecisiones en la medida simultánea
de la posición y el momento lineal de una partícula.
- El principio de incertidumbre de Heisenberg es una consecuencia de la mecánica clásica relativista,
en concreto del hecho de que
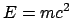 .
.
- La función trabajo de un metal vale 2.6 eV. Se puede extraer un electrón mediante el
efecto fotoeléctrico si se hace incidir sobre el metal:
- Un fotón de energía 1.6 eV.
- Dos fotones de energía 1.6 eV cada uno.
- Un número suficientemente grande de fotones, independientemente de su energía.
- Un fotón de energía 2.8 eV.
- El módulo del momento angular de un electrón en el átomo de hidrógeno
cuando está descrito por el orbital
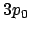 y cuando está descrito por el orbital
y cuando está descrito por el orbital 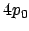 :
:
- Es el mismo en ambos casos y vale
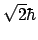 .
.
- Es distinto en un caso que en otro, y vale
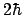 y
y 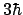 , respectivamente.
, respectivamente.
- Es el mismo en ambos casos y vale
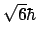 .
.
- Es el mismo en ambos casos y vale 0.
- De los niveles de energía estacionarios de una partícula en una caja monodimensional
de longitud
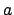 , caracterizados por el número cuántico
, caracterizados por el número cuántico 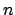 , se puede decir que:
, se puede decir que:
- Están equiespaciados sea cual sea el valor de
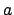 .
.
- El estado fundamental tiene energía cero.
- Su energía es proporcional a
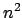 , donde
, donde
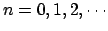 y crece con la longitud de
la caja.
y crece con la longitud de
la caja.
- Su energía es proporcional a
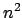 , donde
, donde
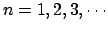 y disminuye con la longitud de
la caja.
y disminuye con la longitud de
la caja.
- En el ion Li
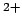 , sin considerar la interacción spin-órbita,
las energías orbitales son:
, sin considerar la interacción spin-órbita,
las energías orbitales son:
- Función de los números cuánticos
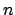 y
y 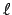 .
.
- Función sólo del número cuántico
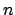 .
.
- Directamente proporcionales al número cuántico
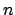 .
.
- Directamente proporcionales al número cuántico
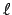 .
.
- La función de onda para el primer estado excitado de un oscilador armónico
monodimensional es de la forma
- La densidad de probabilidad de encontrar a la partícula es nula en
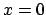 .
.
- La densidad de probabilidad de encontrar a la partícula es máxima en
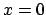 .
.
- La función tiene un mínimo en
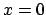 .
.
- La función toma el mismo valor en los puntos
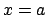 y
y 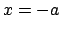 .
.
- Un electrón de un átomo hidrogenoide en un estado enlazado descrito por la función de onda
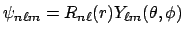 tiene una densidad de
probabilidad radial (o función de distribución radial) proporcional a:
tiene una densidad de
probabilidad radial (o función de distribución radial) proporcional a:
-
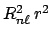
-
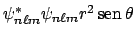
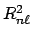
-
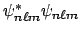
- La función de onda
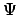 de un sistema confinado debe normalizarse:
de un sistema confinado debe normalizarse:
- Para que se cumpla que
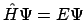 .
.
- Para que
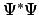 sea una densidad de probabilidad.
sea una densidad de probabilidad.
- Para que se cumpla que
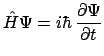 .
.
- Para que
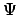 sea continua.
sea continua.
- Los números cuánticos correspondientes al siguiente orbital de un átomo de hidrógeno
son:
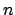 = 1,
= 1, 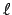 = 1,
= 1, 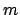 =-1
=-1
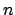 = 2,
= 2, 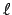 = 1,
= 1, 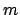 = 1
= 1
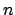 = 2,
= 2, 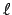 = 1,
= 1, 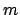 =-1
=-1
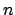 = 3,
= 3, 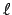 = 0,
= 0, 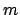 = 0
= 0
- ¿Cuál de las siguientes funciones es antisimétrica respecto
al intercambio de electrones?
-
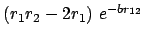
-
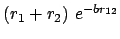
-
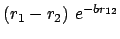
-
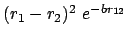
- El segundo estado excitado de una caja cuadrada de lado
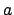 :
:
- Tiene energía
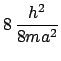 y no está degenerado.
y no está degenerado.
- Tiene energía
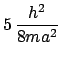 y degeneración 3
y degeneración 3
- Tiene energía
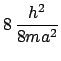 y degeneración 2
y degeneración 2
- Tiene energía
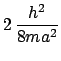 y degeneración 2
y degeneración 2
- El término espectral fundamental para el átomo de Si ([Ne]
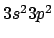 ) es:
) es:
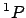
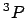
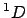
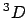
- El hamiltoniano completo de la molécula de HeH
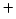 , donde los subíndices 1 y
2 denotan los electrones, es:
, donde los subíndices 1 y
2 denotan los electrones, es:
-
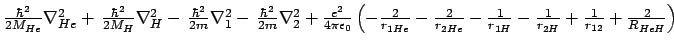
-
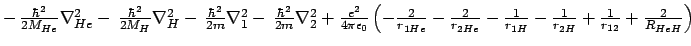
-
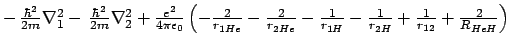
-
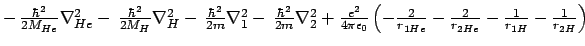
- Para el átomo de Li
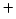 , la función
, la función
- Es la única función de onda válida para cualquier estado electrónico del Li
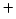 .
.
- Es una solución exacta de la ecuación de Schrödinger independiente del tiempo.
- Describe una función de onda aproximada para el estado fundamental del Li
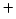 en la aproximación orbital.
en la aproximación orbital.
- Se anula ya que hay dos filas iguales.
- En la aproximación de Born-Oppenheimer, la curva de
energía potencial nuclear
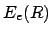 se obtiene:
se obtiene:
- Resolviendo
[
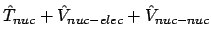 ]
] =
=
 a cada valor de la distancia internuclear
a cada valor de la distancia internuclear 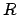 .
.
- Resolviendo
[
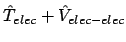 ]
]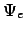 =
= 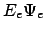 a cada valor de la distancia internuclear
a cada valor de la distancia internuclear 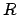 .
.
- Resolviendo
[
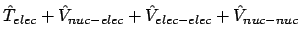 ]
]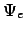 =
= 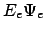 a cada valor de la distancia internuclear
a cada valor de la distancia internuclear 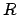 .
.
- Resolviendo
[
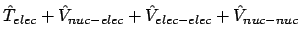 ]
]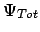 =
=
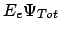 para un único valor de la distancia internuclear
para un único valor de la distancia internuclear 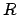 .
.
- ¿Cuál de las siguientes transiciones del espectro electrónico de un átomo
hidrogenoide corresponde a una transición permitida de la serie de Balmer?
- 4
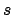
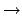 2
2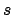
- 3
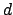
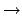 2
2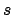
- 4
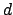
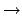 2
2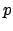
- 4
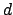
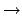 3
3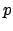
© Copyright.
UAM
2006-10-10


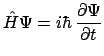 .
.
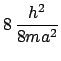 y no está degenerado.
y no está degenerado.
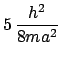 y degeneración 3
y degeneración 3
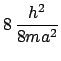 y degeneración 2
y degeneración 2
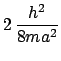 y degeneración 2
y degeneración 2