Puntuación:

- Cada respuesta correcta suma 1/2 punto.
- Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
- Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya
respuesta se conozca con seguridad. Sólo hay una respuesta correcta en
cada pregunta.
En la hoja de respuestas no olvidéis rellenar:
- NOMBRE Y APELLIDOS.
- DNI.
- MODELO (Importante: toda hoja de respuestas sin modelo
equivale a un suspenso).
- La función trabajo de cierto metal es
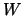 . Si hacemos incidir sobre su superficie
radiación electromagnética de longitud de onda
. Si hacemos incidir sobre su superficie
radiación electromagnética de longitud de onda 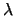 , se emiten electrones.
La energía cinética
, se emiten electrones.
La energía cinética 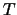 de
los electrones emitidos será:
de
los electrones emitidos será:
-
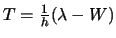
-
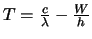
-
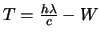
-
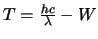
- Las propiedades ondulatorias de una partícula se hacen más patentes:
- al aumentar su velocidad.
- al disminuir su momento lineal.
- al aumentar su energía cinética.
- al disminuir su longitud de onda de de Broglie.
- Se desea medir simultáneamente la posición,
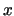 , y el momento lineal,
, y el momento lineal,
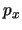 , de una partícula con una precisión
, de una partícula con una precisión 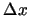 y
y 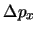 respectivamente.
Sabiendo que
respectivamente.
Sabiendo que 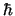 = 1.055
= 1.055 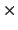 10
10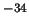 J
J s,
s,
- Ambas magnitudes se pueden medir simultáneamente con tanta precisión como se desee.
- No es posible, en ningún caso, medir las dos variables simultáneamente.
- Es posible obtener una medida con
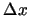 = 10
= 10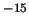 m y
m y 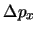 = 10
= 10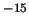 kg m/s
kg m/s
- Es posible obtener una medida con
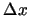 = 10
= 10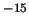 m y
m y 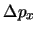 = 10
= 10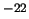 kg m/s
kg m/s
- La función de onda
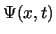 de un estado estacionario de un sistema
de una partícula que se mueve a lo largo del eje
de un estado estacionario de un sistema
de una partícula que se mueve a lo largo del eje 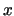 con una
energía potencial independiente del tiempo cumple:
con una
energía potencial independiente del tiempo cumple:
-
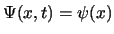
-
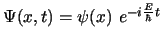
-
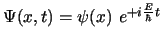
-
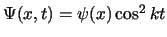
- Una función de onda que sea aceptable para describir un estado cualquiera de un
sistema
- Debe ser independiente del tiempo.
- Puede tomar dos valores distintos en algún punto.
- Es necesario que sea monoevaluada y contínua.
- Es suficiente con que sea compleja y contínua.
- La función de onda para una partícula libre de masa
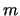 y
energía cinética
y
energía cinética 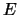 , moviéndose en el eje
, moviéndose en el eje 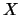 ,
es
,
es
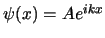 , donde
, donde
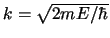 . La densidad de probabilidad
de encontrar a la partícula en un punto del eje
. La densidad de probabilidad
de encontrar a la partícula en un punto del eje 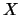 :
:
- Puede ser imaginaria.
- Oscila con
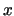 .
.
- Es independiente de
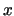 .
.
- Ninguna de las respuestas anteriores es correcta.
- Cuando una partícula en una caja monodimensional de longitud
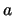 se
encuentra en su estado fundamental, descrita por la función de onda
se
encuentra en su estado fundamental, descrita por la función de onda
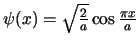 (
(
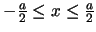 ):
):
- La densidad de probabilidad de encontrarla en
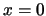 es
es 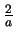 .
.
- La densidad de probabilidad de encontrarla en
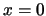 es
es 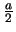 .
.
- La densidad de probabilidad de encontrarla en
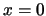 es 0.
es 0.
- La probabilidad de encontrarla en
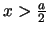 es
mayor que 0.
es
mayor que 0.
- En un oscilador armónico monodimensional, las longitudes de onda de
transición entre dos niveles electrónicos consecutivos (
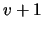 ,
donde
,
donde 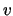 es el número cuántico vibracional)
es el número cuántico vibracional)
- Aumentan al aumentar
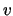 .
.
- Son iguales para todos los valores de
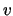 .
.
- Disminuyen al aumentar
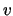 .
.
- Son inversamente proporcionales a la energía de los niveles.
- La función de onda del primer estado excitado de un
oscilador armónico monodimensional tiene la forma (
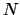 es una constante):
es una constante):
-
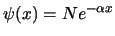
-
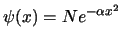
-
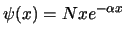
-
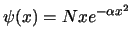
- La probabilidad de que una partícula de masa
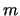 con energía
con energía
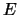 atraviese una barrera de potencial de altura
atraviese una barrera de potencial de altura 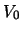 (
(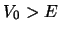 )
y anchura
)
y anchura 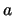 por efecto túnel:
por efecto túnel:
- Aumenta al aumentar la altura de la barrera.
- Disminuye al disminuir la anchura de la barrera.
- Es menor para un protón que para un electrón.
- Es independiente de la energía de la partícula.
- Un nivel de energía de un rotor rígido de masa reducida
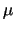 y distancia
y distancia 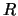 vale
vale
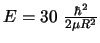 y corresponde a un valor del módulo del momento
angular
y corresponde a un valor del módulo del momento
angular
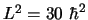 .
.
- Se trata del nivel de número cuántico
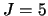 (
(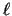 = 5) y no está degenerado.
= 5) y no está degenerado.
- Se trata del nivel de número cuántico
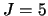 (
(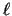 = 5) y contiene 11 estados degenerados.
= 5) y contiene 11 estados degenerados.
- Se trata del nivel de número cuántico
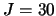 (
(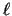 = 30) y no está degenerado.
= 30) y no está degenerado.
- Se trata del nivel de número cuántico
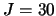 (
(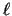 = 30) y contiene 30 estados degenerados.
= 30) y contiene 30 estados degenerados.
- De un electrón que se encuentra en el orbital
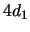 del átomo de hidrógeno
sabemos que
del átomo de hidrógeno
sabemos que
- El módulo de su momento angular orbital vale
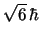 y su componente
y su componente 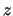 vale
vale
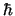 .
.
- El módulo de su momento angular orbital vale
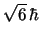 y su componente
y su componente 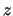 vale
vale
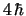 .
.
- El módulo de su momento angular orbital vale
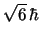 y sus componentes
y sus componentes 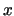 ,
, 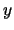 y
y 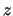 valen
valen
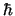 ,
, 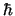 y
y 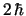 , respectivamente
, respectivamente
- El módulo de su momento angular orbital vale
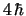 y su componente
y su componente 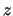 vale
vale
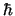 .
.
- Los números cuánticos correspondientes al orbital de un átomo hidrogenoide
siguiente
son:
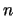 = 3,
= 3, 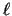 = 2,
= 2, 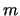 = 0
= 0
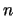 = 2,
= 2, 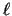 = 3,
= 3, 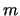 = 0
= 0
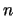 = 3,
= 3, 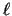 = 2,
= 2, 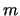 = -1
= -1
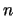 = 3,
= 3, 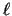 = 1,
= 1, 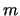 = 0
= 0
- ¿Cuál de las siguientes transiciones entre orbitales de un átomo hidrogenoide
corresponde a una transición permitida de la serie de Balmer?
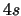
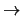
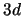
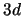
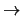
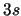
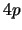
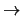
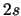
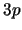
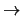
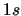
- Cuando se utiliza una función de onda basada en el modelo de electrones
independientes (o aproximación orbital), por ejemplo
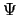 , para describir el estado
fundamental del átomo de He, el valor medio de la energía del sistema
, para describir el estado
fundamental del átomo de He, el valor medio de la energía del sistema
(suponemos que 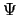 está normalizada) es:
está normalizada) es:
- menor que el valor exacto de la energía del estado fundamental.
- igual que el valor exacto de la energía del estado fundamental.
- mayor que el valor exacto de la energía del estado fundamental.
- igual a la energía del ion He
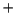 .
.
- ¿Cuál de las siguientes funciones puede usarse para representar correctamente
un estado del átomo de C
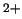 ?
?
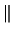
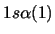
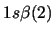
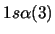
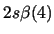
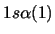
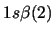
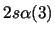
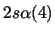
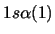
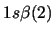
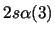
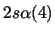
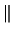
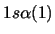
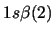
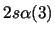
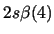
Nota: La nomenclatura
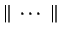 representa un determinante de Slater formado a partir
de los spin-orbitales reseñados.
representa un determinante de Slater formado a partir
de los spin-orbitales reseñados.
- ¿Cuál de las siguientes funciones es antisimétrica respecto
al intercambio de electrones?
-
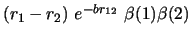
-
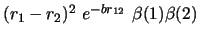
-
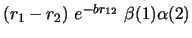
-
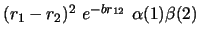
- El hamiltoniano electrónico de la molécula de HeH
 , donde los subíndices 1 y
2 denotan los electrones, es:
, donde los subíndices 1 y
2 denotan los electrones, es:
-
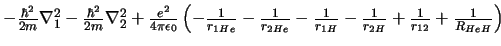
-
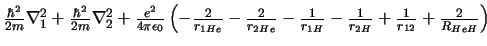
-
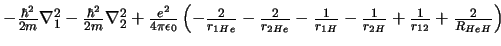
-
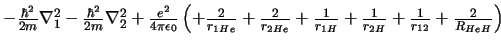
- En la aproximación de Born-Oppenheimer
se considera:
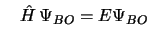 donde tenemos
donde tenemos
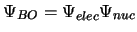 .
.
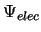 se obtiene fijando las posiciones de los núcleos
y resolviendo
se obtiene fijando las posiciones de los núcleos
y resolviendo
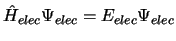 ,
con
,
con
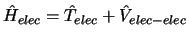
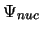 se obtiene fijando las posiciones de los electrones
y resolviendo
se obtiene fijando las posiciones de los electrones
y resolviendo
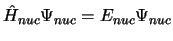 ,
con
,
con
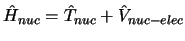
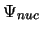 se obtiene fijando las posiciones de los electrones
y resolviendo
se obtiene fijando las posiciones de los electrones
y resolviendo
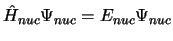 ,
con
,
con
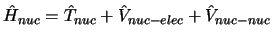
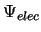 se obtiene fijando las posiciones de los núcleos
y resolviendo
se obtiene fijando las posiciones de los núcleos
y resolviendo
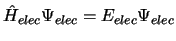 ,
con
,
con
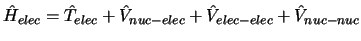 .
.
- El orbital molecular de energía más baja de la
molécula de H
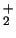 (orbital
(orbital 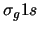 ) es enlazante porque:
) es enlazante porque:
- posee un plano nodal perpendicular al eje internuclear en la zona entre los núcleos.
- disminuye la densidad electrónica en la zona internuclear, respecto a los
átomos separados.
- no varía la densidad electrónica en la zona internuclear, respecto a los
átomos separados.
- aumenta la densidad electrónica en la zona internuclear, respecto a los
átomos separados.
© Copyright.
Noemí Fernández
2004-07-01

