Examen de Fundamentos de Química Cuántica (Junio 2003)

Puntuación:
- Cada respuesta correcta suma 1/2 punto.
- Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
- Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya
respuesta se conozca con seguridad. Sólo hay una respuesta correcta en
cada pregunta.
En la hoja de respuestas no olvidéis rellenar:
- el nombre y apellidos.
- el DNI.
- el MODELO (Importante: toda hoja de respuestas sin modelo
equivale a un suspenso).
- La interpretación de los experimentos de radiación de cuerpo negro
ha sido posible tras aceptar:
- Que la energía de la materia está cuantizada.
- El principio de indeterminación.
- El dualismo onda-corpúsculo.
- Que la energía de la radiación electromagnética está cuantizada.
- Un electrón que se mueve con un momento lineal o cantidad de movimiento
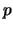 :
:
- Lleva una onda asociada cuya longitud de onda vale
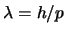 pero no puede medirse.
pero no puede medirse.
- Lleva una onda asociada cuya longitud de onda vale
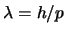 y puede medirse.
y puede medirse.
- Lleva una onda asociada cuya longitud de onda vale
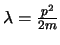 y puede medirse
y puede medirse
- No lleva una onda asociada que pueda medirse.
- El principio de indeterminación de Heisenberg establece que:
- No es posible conocer simultáneamente y con absoluta precisión
la posición y el momento lineal de una partícula.
- Es posible conocer simultáneamente y con absoluta precisión
la posición y el momento lineal de una partícula.
- No es posible conocer con absoluta precisión
la posición de una partícula.
- El momento lineal de una partícula y su posición dependen
de la lontigud de onda.
- La función de onda
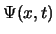 de un estado estacionario
de una partícula que se mueve a lo largo del eje
de un estado estacionario
de una partícula que se mueve a lo largo del eje 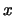 con una energía potencial independiente del tiempo cumple:
con una energía potencial independiente del tiempo cumple:
-
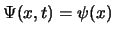
-
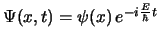
-
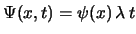
-
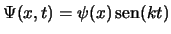
- Una función de onda
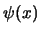 se normaliza para que:
se normaliza para que:
- Su cuadrado complejo
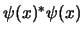 sea proporcional a la densidad de probabilidad de encontrar la partícula en
sea proporcional a la densidad de probabilidad de encontrar la partícula en 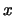 .
.
- Sea una función de onda aceptable.
- Cumpla la Ecuación de Scrhödinger independiente del tiempo.
- Su cuadrado complejo
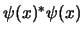 sea igual a la densidad de probabilidad de encontrar la partícula en
sea igual a la densidad de probabilidad de encontrar la partícula en 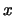 .
.
- En Mecánica Cuántica, a cada propiedad observable corresponde un operador,
cuya expresión:
- Se obtiene a partir su expresión en mecánica clásica en función de
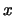 ,
, 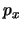 , ...,
aplicando la ecuación de Schrödinger.
, ...,
aplicando la ecuación de Schrödinger.
- Se obtiene a partir del principio de indeterminación de Heisenberg sin
utilizar la mecánica clásica.
- Se obtiene a partir de su expresión en mecánica clásica en función de
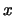 ,
, 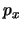 , ...,
sustituyendo
, ...,
sustituyendo
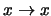 ,
,
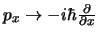 , ...
, ...
- Se postula independientemente para cada observable.
- Cuando una partícula en una caja monodimensional de longitud
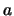 se encuentra en un estado descrito por la función de onda
se encuentra en un estado descrito por la función de onda
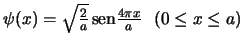 :
:
- La densidad de probabilidad de encontrarla en
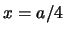 es nula.
es nula.
- La densidad de probabilidad de encontrarla en
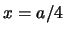 es mayor que en
es mayor que en 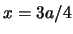 .
.
- La densidad de probabilidad de encontrarla en
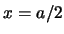 es mayor que en
es mayor que en 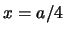 .
.
- La probabilidad de encontrarla en
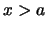 no es nula.
no es nula.
- Los niveles de energía de una partícula en una caja tridimensional
con los tres lados iguales,
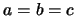 :
:
- Son degenerados si los tres números cuánticos son iguales.
- Tienen una degeneración máxima de 3.
- No pueden ser degenerados.
- Son degenerados si dos de los números cuánticos son distintos.
- En el oscilador armónico monodimensional:
- Todos los niveles de energía son doblemente degenerados.
- Todos los niveles de energía están triplemente degenerados.
- No existe degeneración en ningún nivel de energía.
- No es posible saber si existe degeneración en sus niveles de energía.
- La función de onda del estado fundamental de un oscilador
armónico monodimensional tiene la forma:
-
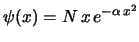 .
.
-
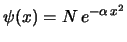 .
.
-
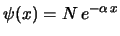 .
.
-
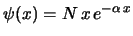 .
.
- El efecto túnel,
dada una barrera de cierta altura y anchura, común para electrones y protones:
- Es más importante en una reacción de transferencia de protones
que en una de transferencia de electrones.
- Tiene la misma importancia en una reacción de transferencia de electrones
que en una de transferencia de protones.
- No tiene ninguna importancia en las reacciones de transferencia de electrones
ni en las de transferencia de protones.
- Es más importante en una reacción de transferencia de electrones
que en una de transferencia de protones.
- El estado estacionario de un rotor rígido
de números cuánticos
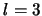 (ó
(ó 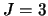 ) y
) y 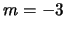 tiene un momento angular
tiene un momento angular
- Cuyo módulo vale
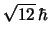 y cuya componente
y cuya componente 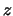 vale
vale 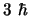 .
.
- Cuyo módulo vale
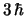 y cuya componente
y cuya componente 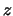 vale
vale 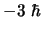 .
.
- Cuyo módulo vale
 y cuya componente
y cuya componente 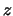 vale
vale 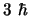 .
.
- Cuyo módulo vale
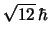 y cuya componente
y cuya componente 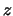 vale
vale 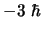 .
.
- Los orbitales
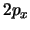 y
y 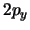 del átomo de hidrógeno:
del átomo de hidrógeno:
- Son funciones propias a la vez de los operadores
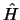 y
y 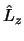 .
.
- Son funciones propias a la vez de los operadores
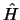 y
y 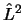 .
.
- Son funciones propias a la vez de los operadores
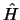 ,
, 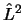 y
y 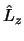 .
.
- Sólo son funciones propias del operador
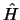 .
.
- Los números cuánticos del orbital del átomo de hidrógeno
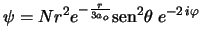 son:
son:
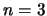 ,
, 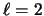 ,
, 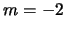 .
.
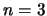 ,
, 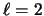 ,
, 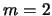 .
.
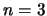 ,
, 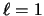 ,
, 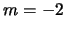 .
.
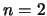 ,
, 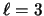 ,
, 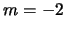 .
.
- La condición de normalización de un orbital hidrogenoide
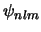 es:
es:
-
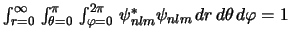 .
.
-
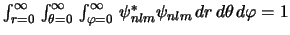 .
.
-
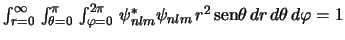 .
.
-
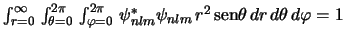 .
.
- En el átomo de He, la función
- Es la solución exacta de la ecuación de Schrödinger que corresponde
al estado fundamental.
- Es la única función aceptable para cualquier estado.
- Tiene dos filas iguales y se anula.
- Es una función aproximada aceptable para el estado fundamental.
- La configuración excitada
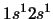 del átomo de He da lugar a:
del átomo de He da lugar a:
- Dos niveles de energía distintos, con un estado cada uno.
- Un nivel de energía con un solo estado.
- Dos niveles de energía distintos, con uno y tres estados respectivamente.
- Un nivel de energía con cuatro estados.
- Sea
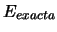 la energía correspondiente a
la solución exacta del estado fundamental del átomo de He.
Si dicho estado se representa con la siguiente
función de onda normalizada:
la energía correspondiente a
la solución exacta del estado fundamental del átomo de He.
Si dicho estado se representa con la siguiente
función de onda normalizada:
en la que
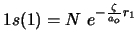 y
y
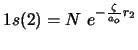 ,
y la energía se calcula utilizando el hamiltoniano exacto
por medio de
,
y la energía se calcula utilizando el hamiltoniano exacto
por medio de
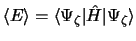 :
:
-
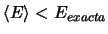 sea cual sea el valor de
sea cual sea el valor de 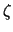 que se elija
que se elija
-
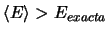 sea cual sea el valor de
sea cual sea el valor de 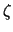 que se elija
que se elija
-
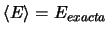 sea cual sea el valor de
sea cual sea el valor de 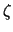 que se elija
que se elija
-
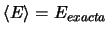 solamente para cierto valor de
solamente para cierto valor de 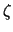
- El Hamiltoniano electrónico de la molécula HeLi
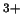 , donde
los subíndices 1 y 2 se refieren a los electrones, es:
, donde
los subíndices 1 y 2 se refieren a los electrones, es:
-
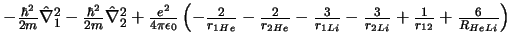
-
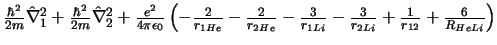
-
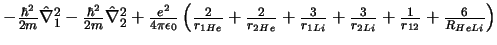
-
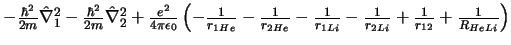
- En la aproximación de Born-Oppenheimer la función de onda molecular se
aproxima como
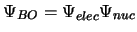 .
En un primer paso:
.
En un primer paso:
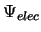 se obtiene fijando las posiciones de los núcleos
y resolviendo
se obtiene fijando las posiciones de los núcleos
y resolviendo
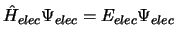 ,
con
,
con
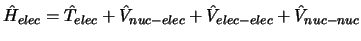
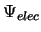 se obtiene fijando las posiciones de los núcleos
y resolviendo
se obtiene fijando las posiciones de los núcleos
y resolviendo
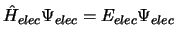 ,
con
,
con
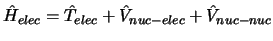
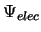 se obtiene fijando las posiciones de los núcleos
y resolviendo
se obtiene fijando las posiciones de los núcleos
y resolviendo
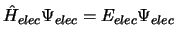 ,
con
,
con
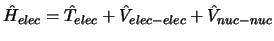
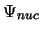 se obtiene fijando las posiciones de los electrones
y resolviendo
se obtiene fijando las posiciones de los electrones
y resolviendo
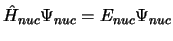 ,
con
,
con
© Copyright.
Noemí Fernández
2003-07-02


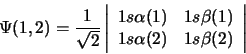
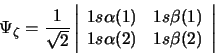
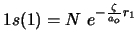 y
y
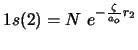 ,
y la energía se calcula utilizando el hamiltoniano exacto
por medio de
,
y la energía se calcula utilizando el hamiltoniano exacto
por medio de