Examen de Fundamentos de Química Cuántica (Junio 2002)
 1
1 de C. Químicas.
de C. Químicas.
Puntuación: 
- Cada respuesta correcta suma 1/2 punto.
- Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
- Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya
respuesta se conozca con seguridad. Sólo hay una respuesta correcta en
cada pregunta.
En la hoja de respuestas no olvidéis rellenar:
- el nombre y apellidos.
- el DNI.
- el MODELO (Importante: toda hoja de respuestas sin modelo
equivale a un suspenso).
- Cuando se produce
el efecto fotoeléctrico, el número de electrones emitido:
- Aumenta al aumentar la longitud de onda de la radiación.
- Aumenta al aumentar la frecuencia de la radiación incidente.
- Aumenta al aumentar la intensidad de la radiación incidente.
- Es proporcional a la raíz cuadrada del potencial de parada.
- En un experimento de difracción de electrones,
la onda asociada a los mismos tiene una longitud de onda
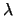 .
El módulo de su momento lineal:
.
El módulo de su momento lineal:
- Es
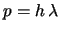 .
.
- Es
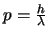 .
.
- Cumple
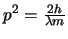 .
.
- Los electrones no son ondas y no experimentan el fenómeno de la difracción.
- Una consecuencia del principio de indeterminación de Heisenberg es
que:
- La posición de una partícula nunca puede conocerse con total
precisión.
- El momento lineal de una partícula nunca puede conocerse con total
precisión.
- Si en un instante dado se conociera con total precisión la posición de una
partícula, el valor de su momento lineal en ese instante se
desconocería completamente.
- Si en un instante dado se conoce con total precisión la posición de una
partícula, el valor de su momento lineal en ese instante
también puede conocerse con total precisión.
- En Mecánica Cuántica,
un estado cualquiera de un sistema de varias partículas queda
definido por:
- Una función de las coordenadas de todas las partículas
y del tiempo.
- Un operador.
- Las posiciones y las velocidades de todas las partículas.
- Una función de las coordenadas de todas las partículas.
- La función de onda que describe un estado estacionario de un
sistema:
- Depende de las coordenadas de las partículas y del tiempo,
y su módulo al cuadrado también.
- Es independiente del tiempo.
- Es nula, porque ningún sistema tiene estados estacionarios.
- Depende de las coordenadas de las partículas y del tiempo,
pero su módulo al cuadrado no depende del tiempo.
- En Mecánica Cuántica, a cada propiedad observable corresponde un operador,
cuya expresión:
- Se postula independientemente para cada observable.
- Se obtiene a partir de su expresión en función de
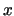 ,
, 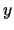 ,
, 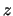 ,
, 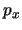 ,
, 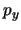 ,
, 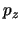 en mecánica clásica.
en mecánica clásica.
- Se deduce de la ecuación de Schrödinger dependiente del tiempo.
- Se deduce del principio de indeterminación de Heisenberg.
- Las soluciones de la ecuación de Schrödinger independiente del
tiempo de un sistema son
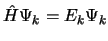 ,
con
,
con
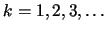 Si el sistema se encuentra en el estado estacionario
Si el sistema se encuentra en el estado estacionario 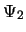 y
se mide su energía una sola vez:
y
se mide su energía una sola vez:
- Se puede obtener cualquiera de los valores
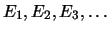 , todos con igual probabilidad.
, todos con igual probabilidad.
- Se puede obtener cualquiera de los valores
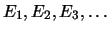 , aunque es más probable obtener
, aunque es más probable obtener
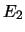 que cualquier otro.
que cualquier otro.
- Se obtiene el valor
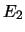 , con toda certeza.
, con toda certeza.
- Se puede obtener cualquier valor, aunque no sea uno de los
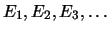 .
.
- Al resolver la ecuación de Schrödinger independiente del tiempo de una
caja monodimensional limitada por
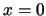 y
y 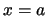 ,
imponiendo que
,
imponiendo que 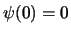 y
y 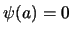 se obtiene:
se obtiene:
- Que la energía de los estados estacionarios es
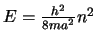 , con
, con
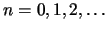 .
.
- Que la energía de los estados estacionarios es
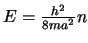 , con
, con
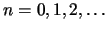 .
.
- Que la energía de los estados estacionarios es
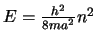 , con
, con
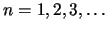 .
.
- Que la energía de los estados estacionarios es
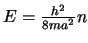 , con
, con
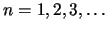 .
.
- En una caja de dos dimensiones en la que
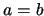 :
:
- Los niveles (
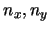 ) con
) con 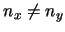 tienen degeneración 2.
tienen degeneración 2.
- Los niveles (
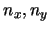 ) con
) con 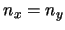 tienen degeneración 2.
tienen degeneración 2.
- Todos los niveles de energía tienen degeneración 2.
- No hay niveles de energía degenerados.
- Los niveles de energía de un oscilador armónico monodimensional
de masa
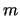 y constante de fuerza
y constante de fuerza 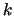 vienen dados por:
vienen dados por:
-
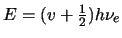 , con
, con
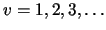 ,
en donde
,
en donde
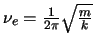 .
.
-
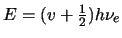 , con
, con
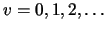 ,
en donde
,
en donde
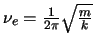 .
.
-
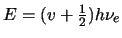 , con
, con
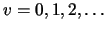 ,
en donde
,
en donde
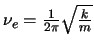 .
.
-
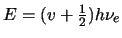 , con
, con 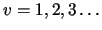 ,
en donde
,
en donde
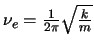 .
.
- La probabilidad de que una partícula de masa
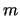 atraviese una barrera de potencial de altura
atraviese una barrera de potencial de altura 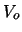 y
anchura
y
anchura 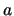 :
:
- Es independiente de la energía de la partícula.
- Aumenta al disminuir la altura de la barrera.
- Aumenta al aumentar la masa de la partícula.
- Aumenta al aumentar la anchura de la barrera.
- El estado
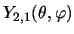 [o
[o
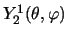 ]
de un rotor rígido:
]
de un rotor rígido:
- Tiene un momento angular de módulo:
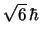 y componente
y componente 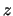 :
: 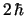 .
.
- Tiene un momento angular de módulo:
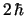 y componente
y componente 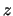 :
: 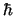 .
.
- Tiene un momento angular de módulo:
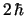 y componente
y componente 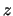 :
: 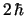 .
.
- Tiene un momento angular de módulo:
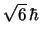 y componente
y componente 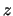 :
: 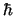 .
.
- Los orbitales
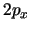 y
y 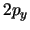 de los átomos hidrogenoides:
de los átomos hidrogenoides:
- Resultan de combinar linealmente los
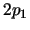 y
y 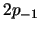 y tienen la misma energía que éstos.
y tienen la misma energía que éstos.
- Son orbitales reales que, a diferencia de los
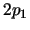 y
y 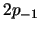 , no cumplen la Ecuación de Schrödinger independiente
del tiempo.
, no cumplen la Ecuación de Schrödinger independiente
del tiempo.
- Son orbitales reales que se postulan por
intuición, sin una base teórica.
- Hacen que, junto con los
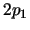 ,
, 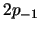 y
y 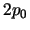 ,
la subcapa
,
la subcapa 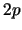 tenga una degeneración de 5.
tenga una degeneración de 5.
- Para un electrón en el átomo de hidrógeno en un estado descrito
por la función de onda normalizada
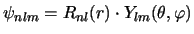 [ o
[ o
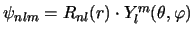 ],
la densidad de probabilidad en el punto
],
la densidad de probabilidad en el punto
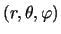 vale:
vale:
-
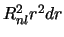
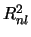
-
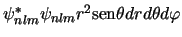
-
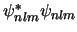
- El valor absoluto de la energía de un átomo hidrogenoide en un
estado descrito por los números cuánticos
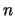 ,
, 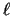 y
y 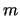 :
:
- Es proporcional a
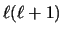 .
.
- Es proporcional a
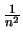 .
.
- Es proporcional a
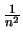 y a
y a 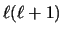 .
.
- Depende de
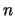 ,
, 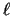 y
y 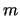 .
.
- La configuración excitada
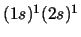 del Li
del Li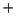 da lugar a:
da lugar a:
- Un único término espectral
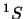 con un solo estado.
con un solo estado.
- Un término espectral
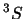 con degeneración 3 y
otro término espectral
con degeneración 3 y
otro término espectral 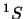 con un solo estado.
con un solo estado.
- Un único término espectral
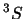 con degeneración 3.
con degeneración 3.
- Cuatro estados con cuatro energías diferentes.
- ¿Cuál de las siguientes funciones de dos electrones
cumple el principio de exclusión de Pauli?
-

-
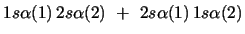
-
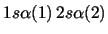
-
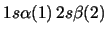
- El fundamento del método variacional es la propiedad de que,
si un sistema tiene un hamiltoniano
 y la energía
de su estado fundamental es
y la energía
de su estado fundamental es 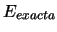 , toda función de
onda normalizada aproximada
, toda función de
onda normalizada aproximada 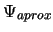 cumple:
cumple:
-
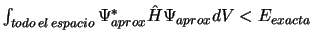 .
.
-
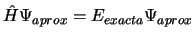 .
.
-
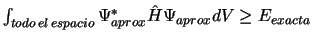 .
.
-
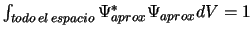 .
.
- El Hamiltoniano electrónico de la molécula LiH
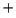 , donde
los subíndices 1, 2 y 3 se refieren a los electrones, es:
, donde
los subíndices 1, 2 y 3 se refieren a los electrones, es:
-
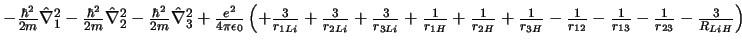
-
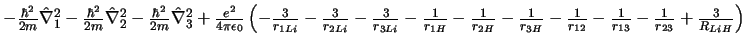
-
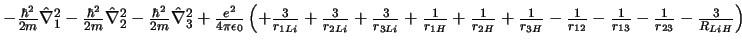
-
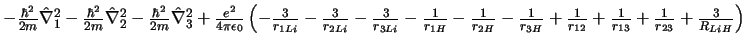
- La configuración electrónica más estable de la molécula de Be
 y su orden de enlace son:
y su orden de enlace son:
-
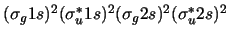 ,
con orden de enlace 2.
,
con orden de enlace 2.
-
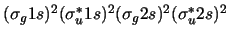 ,
con orden de enlace 0.
,
con orden de enlace 0.
-
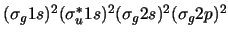 ,
con orden de enlace 2.
,
con orden de enlace 2.
-
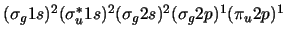 ,
con orden de enlace 2.
,
con orden de enlace 2.
© Copyright.
Cristina Sanz Sanz
2002-07-15
![]()