Examen de Fundamentos de Química Cuántica (Junio 2001)
 1
1 de C. Químicas.
de C. Químicas.
Puntuación: 
- Cada respuesta correcta suma 1/2 punto.
- Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
- Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya
respuesta se conozca con seguridad. Sólo hay una respuesta correcta en
cada pregunta.
En la hoja de respuestas no olvidéis rellenar:
- el nombre y apellidos.
- el DNI.
- el MODELO (Importante: toda hoja de respuestas sin modelo
equivale a un suspenso).
- El efecto fotoeléctrico y la difracción de electrones son
manifestaciones:
- de la naturaleza ondulatoria de la radiación electromagnética
y la naturaleza corpuscular de la materia,
respectivamente,
- de la naturaleza corpuscular de la radiación electromagnética
y la naturaleza ondulatoria de la materia, respectivamente,
- de la naturaleza esencialmente diferente de la materia y de la
radiación electromagnética,
- de que la energía de la radiación electromagnética
es proporcional al cuadrado de la amplitud.
- Un electrón se mueve en la dirección
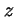 y por lo tanto tiene
una componente
y por lo tanto tiene
una componente 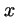 del momento lineal
del momento lineal
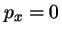 , completamente conocida.
Al medir su coordenada
, completamente conocida.
Al medir su coordenada 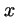 con una precisión
con una precisión 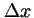 :
:
- Adquiere un
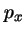 que no se puede conocer con total precisión.
El error en
que no se puede conocer con total precisión.
El error en 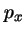 ,
, 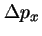 , es tanto mayor cuanto mayor sea
, es tanto mayor cuanto mayor sea 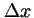 .
.
- Su
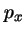 sigue siendo
sigue siendo 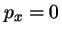 y por lo tanto completamente conocido.
y por lo tanto completamente conocido.
- Adquiere un
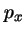 que no se puede conocer con total precisión.
El error en
que no se puede conocer con total precisión.
El error en 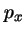 ,
, 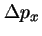 , es tanto mayor cuanto menor sea
, es tanto mayor cuanto menor sea 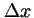 .
.
- La imprecisión en la medida de
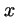 siempre es infinita.
siempre es infinita.
- En Mecánica Cuántica,
un estado de un sistema está definido por:
- Las posiciones y las velocidades de todas las partículas.
- Un operador.
- Una función de las posiciones de todas las partículas
y del tiempo.
- Una ecuación de autovalores o valores propios.
- Cuando un sistema está en un estado
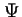 estacionario:
estacionario:
- Su energía es constante y su valor
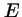 se obtiene de la
ecuación
se obtiene de la
ecuación
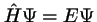 .
.
- Su energía
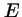 se obtiene de la
ecuación
se obtiene de la
ecuación
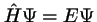 y es una función del tiempo.
y es una función del tiempo.
- Su energía no se puede conocer.
- Un sistema cuántico nunca puede estar en un estado estacionario.
- La función de onda
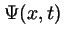 de un estado estacionario
de una partícula que se mueve a lo largo del eje
de un estado estacionario
de una partícula que se mueve a lo largo del eje 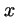 con una energía potencial independiente del tiempo:
con una energía potencial independiente del tiempo:
- Cumple
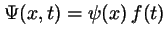 , pero la función
, pero la función
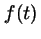 es desconocida.
es desconocida.
- No se puede factorizar nunca como el producto de una función de
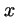 por otra de
por otra de 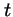 :
:
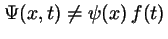 .
.
- Tiene un complejo conjugado independiente del tiempo:
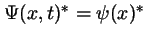
- Cumple
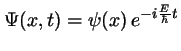 y
y 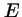 es su energía total.
es su energía total.
- La cuantización de la energía de un sistema:
- Es consecuencia del confinamiento de las partículas que lo
constituyen.
- Aparece al normalizar la función de onda.
- Aparece cuando el sistema está sometido a un potencial constante.
- Es consecuencia de las interacciones culombianas (electrostáticas)
entre las partículas.
- Elige la afirmación que sea correcta:
- En una caja de dos dimensiones los estados (
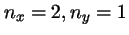 )
y (
)
y (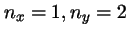 ) son degenerados independientemente de la forma
de la caja.
) son degenerados independientemente de la forma
de la caja.
- En una caja de dos dimensiones los estados (
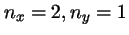 )
y (
)
y (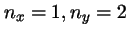 ) son degenerados si los dos lados de la caja son iguales.
) son degenerados si los dos lados de la caja son iguales.
- En una caja de dos dimensiones no puede haber estados degenerados.
- En una caja de una dimensión puede haber estados degenerados.
- En una molécula diatómica el movimiento relativo de los núcleos
corresponde a una vibración.
Por tanto, la energía asociada
a ese movimiento:
- Está cuantizada y no puede ser nula.
- Está cuantizada y es nula en el estado de energía más baja.
- No está cuantizada. Puede tomar cualquier valor por encima de
cierto umbral llamado energía del punto cero.
- Puede tomar cualquier valor real mayor o igual que cero.
- Un oscilador armónico se halla en un estado estacionario
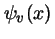 con energía total
con energía total 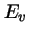 .
Si
.
Si 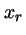 es tal que
es tal que
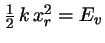 (punto de
retroceso clásico):
(punto de
retroceso clásico):
-
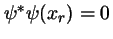 .
.
-
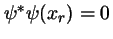 y
y
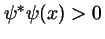 para
para 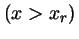 .
.
-
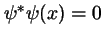 para
para 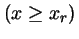 .
.
-
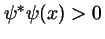 para
para 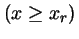 .
.
- La probabilidad de que una partícula que lleva una energía
cinética dada (
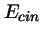 ) atraviese una barrera de energía
potencial superior (
) atraviese una barrera de energía
potencial superior (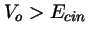 ) y de anchura
) y de anchura 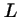 :
:
- Es tanto menor cuanto menor sea la altura de la barrera,
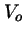 .
.
- Es tanto mayor cuanto mayor sea la anchura de la barrera,
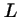 .
.
- Es cero.
- Es tanto mayor cuanto menor sea la masa de la partícula.
- El segundo nivel excitado de un rotor rígido
de masa reducida
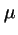 y distancia de giro
y distancia de giro 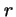 :
:
- Tiene energía
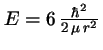 y no es degenerado.
y no es degenerado.
- Tiene energía
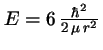 y degeneración 5.
y degeneración 5.
- Tiene energía
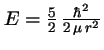 y degeneración 5.
y degeneración 5.
- Tiene energía
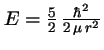 y no es degenerado.
y no es degenerado.
- El modulo del momento angular de un electrón en el átomo de hidrógeno
cuando está en el orbital
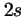 y cuando está en el
y cuando está en el 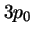 :
:
- Vale cero en ambos casos.
- Vale
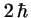 en el primer caso y
en el primer caso y 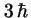 en el segundo.
en el segundo.
- Vale cero en el primer caso y
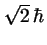 en el segundo.
en el segundo.
- No se puede saber cuánto vale en ninguno de los dos casos.
- Indica cuál de las siguientes afirmaciones es cierta para la
función de onda de un átomo de hidrogenoide:
-
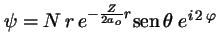 corresponde a
corresponde a 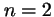 ,
, 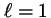 ,
, 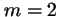 .
.
-
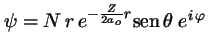 corresponde a
corresponde a 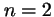 ,
, 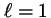 ,
, 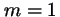
-
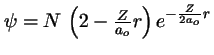 corresponde a
corresponde a 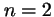 ,
, 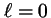 ,
, 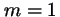
-
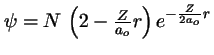 corresponde a
corresponde a 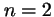 ,
, 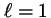 ,
, 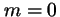
- Los orbitales reales
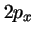 y
y 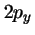 de los átomos hidrogenoides
(que son combinaciones lineales de los
de los átomos hidrogenoides
(que son combinaciones lineales de los 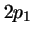 y
y 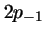 ):
):
- Son funciones propias de los operadores
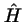 y
y 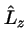
- Sólo son funciones propias de
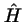
- Son funciones propias de los operadores
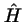 y
y 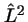
- No son funciones propias ni de
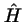 ni de
ni de 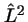 ni de
ni de 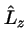
- Para un electrón en el átomo de hidrógeno
en un orbital
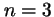 ,
, 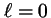 ,
, 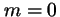 ,
la densidad de probabilidad a una distancia dada del núcleo:
,
la densidad de probabilidad a una distancia dada del núcleo:
- Es la misma para todos los valores posibles de
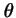 y
y 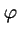 .
.
- Es mayor para
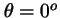 (lado positivo del eje
(lado positivo del eje 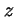 )
que en cualquier otra dirección.
)
que en cualquier otra dirección.
- Es mayor para
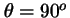 (plano
(plano 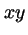 ) que para cualquier otro
valor de
) que para cualquier otro
valor de 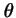 .
.
- Es negativa si
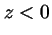 .
.
- La configuración excitada
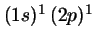 del átomo de He
da lugar a:
del átomo de He
da lugar a:
- Un término espectral más estable,
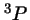 , y otro menos
estable
, y otro menos
estable 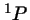 .
.
- Un solo término espectral
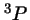 .
.
- Un solo término espectral
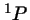 .
.
- Un estado no degenerado
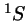 .
.
- Cuál de las siguientes funciones de dos electrones
cumple el Principio de Pauli?
-
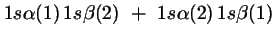
-
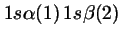
-
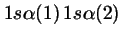
-

- Cuando se usa una función aproximada
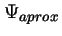 , normalizada, para
describir el estado fundamental del átomo de He, el valor
promedio de la energía con el Hamiltoniano completo del
sistema,
, normalizada, para
describir el estado fundamental del átomo de He, el valor
promedio de la energía con el Hamiltoniano completo del
sistema,
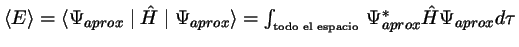 :
:
- Es menor que el valor exacto de la energía del estado fundamental.
- Coincide siempre con el valor exacto de la energía del estado fundamental.
- Es mayor o igual que el valor exacto de la energía del estado fundamental.
- Es igual a la energía del ion He
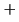 .
.
- De acuerdo con la aproximación de Born-Oppenheimer,
la distancia de enlace o distancia de equilibrio de una molécula
diatómica es aquella en la que:
- La repulsión internuclear es mínima.
- La energía potencial nuclear es mínima.
- La energía electrónica es máxima.
- La molécula puede permanecer indefinidamente con los núcleos
inmóviles.
- El estado de transición para una reacción
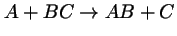 es:
es:
- Un mínimo de la superficie de energía potencial nuclear.
- Un punto de silla de la superficie de energía potencial nuclear.
- Un máximo de la superficie de energía potencial nuclear.
- Un punto cualquiera de la superficie de energía potencial nuclear.
© Copyright.
Cristina Sanz Sanz
2002-04-02
![]()
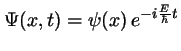 y
y 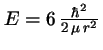 y no es degenerado.
y no es degenerado.
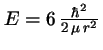 y degeneración 5.
y degeneración 5.
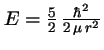 y degeneración 5.
y degeneración 5.
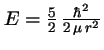 y no es degenerado.
y no es degenerado.
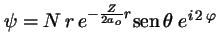 corresponde a
corresponde a 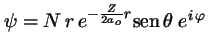 corresponde a
corresponde a 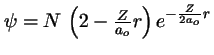 corresponde a
corresponde a 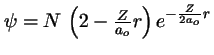 corresponde a
corresponde a