Examen de Fundamentos de Química Cuántica (Junio 2000)
 1
1 de C. Químicas.
de C. Químicas.
Puntuación: 
- Cada respuesta correcta suma 1/2 punto.
- Cada respuesta incorrecta (o múltiple) resta 1/6 punto.
- Cada pregunta no contestada no puntúa.
Resulta conveniente contestar solamente aquellas preguntas cuya
respuesta se conozca con seguridad. Sólo hay una respuesta correcta en
cada pregunta.
En la hoja de respuestas no olvidéis rellenar:
- el nombre y apellidos.
- el DNI.
- el MODELO (Importante: toda hoja de respuestas sin modelo
equivale a un suspenso).
- La frecuencia umbral para la emisión fotoelectrónica de un
determinado metal es 0.9
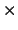 10
10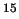 s
s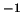 . Indicar qué
radiación es capaz de producir el efecto fotoeléctrico,
sabiendo que
. Indicar qué
radiación es capaz de producir el efecto fotoeléctrico,
sabiendo que
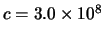 m/s:
m/s:
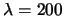 nm
nm
-
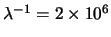 m
m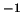
-
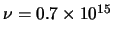 s
s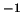
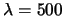 nm
nm
- Cuál de las siguientes afirmaciones es cierta?
- La posición o el momento lineal de una partícula nunca se pueden medir.
- La naturaleza ondulatoria de la materia conduce a
indeterminaciones en la medida simultánea de la posición y el
momento lineal de una partícula.
- El principio de indeterminación de Heisenberg es una
consecuencia de la mecánica clásica relativista, en particular de
que
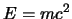 .
.
- La posición y el momento lineal de una partícula
microscópica pueden conocerse con total precisión en determinadas
circunstancias si se dispone del instrumental experimental adecuado.
- Según la dualidad onda-corpúsculo, un electrón
- Describe trayectorias descritas por la ecuación
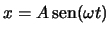 .
.
- Tiene cuantizado su momento lineal.
- Su masa depende de su longitud de onda.
- Su momento lineal está relacionado con su longitud de onda asociada.
- La ecuación
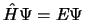
- Implica que
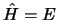 .
.
- La cumplen solamente los estados estacionarios de un sistema si la
energía potencial no depende del tiempo.
- La cumplen todos los estados de un sistema, estacionarios o
no estacionarios.
- La cumple solamente los estados de un sistema con funciones de
onda antisimétricas.
- Si
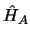 y
y 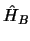 son dos hamiltonianos independientes,
tales que
son dos hamiltonianos independientes,
tales que
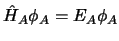 y
y
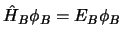 ,
y
,
y
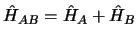 ,
cuya ecuación de valores propios es
,
cuya ecuación de valores propios es
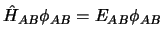 ,
se cumple que:
,
se cumple que:
-
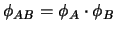 y
y
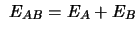 .
.
-
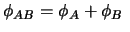 y
y
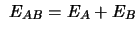 .
.
-
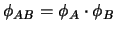 y
y
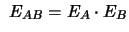 .
.
-
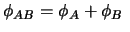 y
y
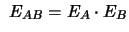 .
.
- Según la mecánica cuántica:
- A cada estado de un sistema se asocia un operador.
- A cada observable de un sistema se asocia un operador.
- A cada estado se asocia un observable.
- Los conceptos de estado y de observable carecen de significado físico.
- La probabilidad de encontrar una partícula en una región
del espacio:
- Depende del tiempo si el estado es estacionario.
- Nunca depende del tamaño de la región.
- Es siempre nula.
- Es independiente del tiempo si el estado es estacionario.
- La ecuación de Schrödinger independiente del tiempo de una
caja monodimensional,
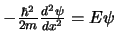 ,
se puede expresar
,
se puede expresar
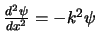 ,
con
,
con
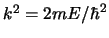 .
Las soluciones de dicha ecuación diferencial son las funciones
.
Las soluciones de dicha ecuación diferencial son las funciones
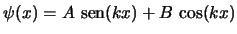 .
La cuantización de la energía surge de:
.
La cuantización de la energía surge de:
- Sustituir
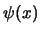 en la ecuación diferencial.
en la ecuación diferencial.
- Imponer que
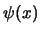 esté normalizada.
esté normalizada.
- Imponer que
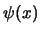 se anule en los límites de la caja.
se anule en los límites de la caja.
- Hacer
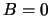 porque el valor exacto de
porque el valor exacto de 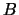 es muy pequeño y
se comete poco error al despreciarlo.
es muy pequeño y
se comete poco error al despreciarlo.
- Los niveles de energía vibracional de un oscilador armónico
monodimensional
de frecuencia de vibración clásica (o frecuencia de vibración
fundamental)
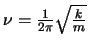 ,
,
- Están equiespaciados, no tienen degeneración y la
energía del estado fundamental es
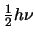 .
.
- Están equiespaciados y todos son degenerados excepto el estado
fundamental, cuya energía es
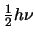 .
.
- No tienen degeneración y la separación entre un nivel y el
siguiente tiende a ser nula cuando el número cuántico
vibracional tiende a infinito.
- Varían de forma continua.
- La probabilidad de que una partícula con energía
cinética dada (
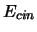 ) atraviese una barrera de energía
potencial mayor (
) atraviese una barrera de energía
potencial mayor (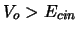 ) y de anchura
) y de anchura 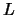 ,
,
- Es nula.
- Aumenta al aumentar la altura de la barrera,
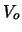 .
.
- Aumenta al disminuir la anchura de la barrera,
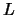 .
.
- Aumenta al aumentar la masa de la partícula.
- En un átomo hidrogenoide, la energía de un estado
descrito por los números cuánticos
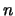 ,
, 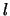 y
y 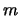 :
:
- Depende de
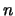 y
y 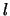 pero no de
pero no de 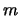 .
.
- Es proporcional a
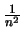 e independiente de
e independiente de 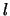 y
y 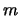 .
.
- Sólo depende de
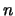 y es proporcional a
y es proporcional a 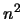 .
.
- Sólo depende de
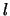 y es proporcional a
y es proporcional a 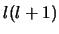 .
.
- Un electrón en un átomo de hidrógeno se encuentra en el nivel
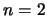 .
.
- Existen estados de diferente energía en ese nivel.
- Todos los estados tienen el mismo valor del momento angular.
- Todos los estados tienen la misma energía.
- Sólo existe un estado en ese nivel.
- La proyección sobre el eje
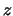 del
momento angular de un electrón en el átomo de hidrógeno cuando
está en un orbital
del
momento angular de un electrón en el átomo de hidrógeno cuando
está en un orbital 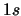 y cuando está en un orbital
y cuando está en un orbital 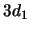 :
:
- Es
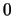 y
y 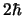 , respectivamente.
, respectivamente.
- Es
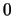 y
y 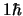 , respectivamente.
, respectivamente.
- Es
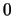 y
y
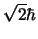 , respectivamente.
, respectivamente.
- No se puede saber cuanto vale en ninguno de los dos casos.
- Un electrón se encuentra en el estado
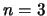 ,
, 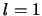 ,
, 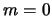 del
átomo de hidrógeno.
del
átomo de hidrógeno.
- La densidad de probabilidad es la misma en cualquier dirección.
- La densidad de probabilidad es negativa si
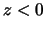 .
.
- La densidad de probabilidad sólo depende de la distancia entre
el electrón y el protón.
- La densidad de probabilidad es mayor en la dirección del eje
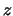 que en cualquier otra dirección.
que en cualquier otra dirección.
- La configuración excitada
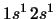 del átomo de He
da lugar a:
del átomo de He
da lugar a:
- Un estado no degenerado
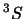 .
.
- Cuatro estados de igual energía.
- Cuatro estados agrupados en dos niveles o términos espectrales:
uno triplemente degenerado,
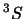 , y otro no degenerado,
, y otro no degenerado, 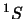 .
.
- Cuatro estados con cuatro energías diferentes.
- De las siguientes funciones, cuál puede usarse para representar
correctamente un estado del átomo de Li?
-
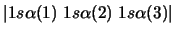
-
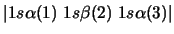
-
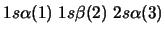
-
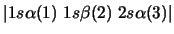
- Una configuración de un átomo contiene un término
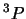 .
Dicho término consta de:
.
Dicho término consta de:
- Un estado no degenerado
en el que todos los electrones están desapareados.
- Nueve estados degenerados,
cada uno de ellos con un valor diferente del
momento angular orbital y del momento angular de spin.
- Nueve estados degenerados,
con valores comunes de
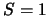 y
y 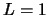 y
con valores de
y
con valores de 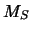 y
y 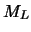 diferentes.
diferentes.
- Tres estados de igual energía.
- De acuerdo con la aproximación de Born-Oppenheimer,
la distancia de enlace o distancia de equilibrio de una molécula
diatómica es aquella en la que:
- La repulsión internuclear es mínima.
- Los dos átomos están infinitamente separados.
- La molécula puede permanecer indefinidamente con los núcleos
inmóviles.
- La energía potencial nuclear (suma de la energía
electrónica y la repulsión internuclear) es mínima.
- El Hamiltoniano electrónico de la molécula LiH
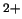 , donde
los subíndices 1 y 2 se refieren a los electrones, es:
, donde
los subíndices 1 y 2 se refieren a los electrones, es:
-
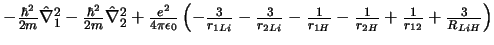
-
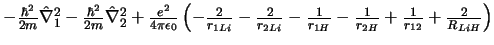
-
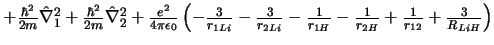
-
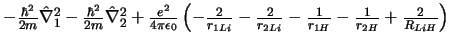
- Cuál de las siguientes funciones de dos electrones
es antisimétrica con respecto al intercambio de los dos electrones?
-
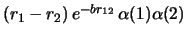
-
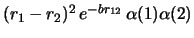
-
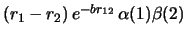
-
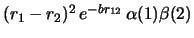
© Copyright.
Cristina Sanz Sanz
2001-05-17
![]()