
 0
0 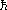 2) /
(me e2) en el Sistema MKSC.
2) /
(me e2) en el Sistema MKSC.
Datos: h = 6.6261x10-34 J.s., c = 2.9979x108 m/s, e = 1.6022x10-19 C, ao = 5.2918x10-11m, me = 9.1094x10-31 Kg.
a0 = (4 
 0
0 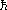 2) /
(me e2) en el Sistema MKSC.
2) /
(me e2) en el Sistema MKSC.
Algunas Integrales que se pueden usar con los problemas anteriores:
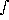
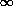 o
e-b x2 dx = 1/2 (
o
e-b x2 dx = 1/2 ( /b)1/2
/b)1/2
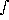
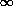 o
x2 e-b x2 dx = 1/4 (
o
x2 e-b x2 dx = 1/4 ( /b3)1/2
/b3)1/2
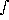
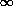 t
r2 e-a r dr =
(1 + at + a2t2/2)
e-a t /a3
t
r2 e-a r dr =
(1 + at + a2t2/2)
e-a t /a3
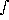
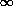 o
xn e-qx dx = n!/qn+1 , n>-1 , q>0
o
xn e-qx dx = n!/qn+1 , n>-1 , q>0
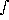 r2 ea r dr =
(r2 -2r/a + 2/a2) ea r/a
r2 ea r dr =
(r2 -2r/a + 2/a2) ea r/a
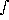 x sen2 ax .dx = x2/4 - (cos 2ax)/8a2
x sen2 ax .dx = x2/4 - (cos 2ax)/8a2
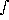 sen2 ax .dx = x/2 - ((sen 2ax)/(4a))
sen2 ax .dx = x/2 - ((sen 2ax)/(4a))
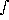 2
2 o
sen2
o
sen2 d
d
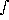
 o
sen2
o
sen2 d
d =
2
=
2 /3
/3
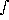 sen(ax) sen(bx) dx = 1/2 [ (sen(a-b)x)/(a-b)
- (sen(a+b)x)/(a+b) ]
sen(ax) sen(bx) dx = 1/2 [ (sen(a-b)x)/(a-b)
- (sen(a+b)x)/(a+b) ]
Operador "Nabla cuadrado" en polares. Nota: todas las derivadas son parciales, pero no tengo el "simbolito" a mano.
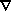 2 =
(1/r2 d/dr (r2 d/dr)) +
(1/(r2 sen
2 =
(1/r2 d/dr (r2 d/dr)) +
(1/(r2 sen ) d/d
) d/d (sen
(sen d/d
d/d )) +
(1/(r2 sen2
)) +
(1/(r2 sen2 ) d2/d
) d2/d 2)
2)