Fundamentos de Química Cuántica
1 de Ciencias Químicas
de Ciencias Químicas
Examen 13 de septiembre 2007 (problemas)
- Una partícula de masa
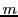 se encuentra en una caja bidimensional
de potencial infinito de lados
se encuentra en una caja bidimensional
de potencial infinito de lados 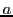 y
y 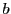 , con
, con 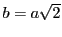 .
.
- Obtener la función de onda normalizada que es solución de la ecuación
de Schrödinger independiente del tiempo para dicha partícula.
- Obtener, sustituyendo la función de onda en la ecuación de Schrödinger,
la expresión de la energía para un estado con números cuánticos
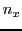 y
y 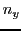 .
.
- Haz un diagrama mostrando los 5 niveles energéticos de menor energía, e indica su
degeneración.
Datos:
Las soluciones de la ecuación de Schrödinger independiente del tiempo para una
partícula en una caja de potencial monodimensional de longitud 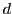 tienen la forma:
tienen la forma:
- La función de onda normalizada
del estado fundamental de un oscilador armónico de masa
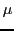 y constante de fuerza
y constante de fuerza 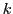 es
es
- Representar las gráficas de las funciones
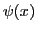 y
y 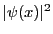 ,
junto con la curva de energía potencial del sistema,
,
junto con la curva de energía potencial del sistema,
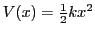 .
.
- Calcular el valor medio de la posición
 .
.
- Calcular la probabilidad de encontrar la partícula en la mitad derecha (
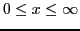 ).
).
- Calcular la densidad de probabilidad de encontrar la partícula en
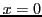 .
.
Datos:
- Responder brevemente a las siguientes preguntas:
- Para el catión Be
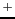 en su estado fundamental
en su estado fundamental
- Escribir el hamiltoniano.
- Escribir una función de onda que represente correctamente el catión con una configuración
electrónica
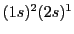 .
.
- Obtener los términos espectrales correspondientes a dicha configuración.
- Para el átomo de Be en su configuración excitada
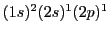 .
.
- Obtener los términos espectrales permitidos.
- Ordenar los términos por orden creciente de energías usando las
reglas de Hund, suponiendo que se pueden aplicar en este caso.
2008-07-02
![]() de Ciencias Químicas
de Ciencias Químicas
![]() tienen la forma:
tienen la forma: