Sea un sistema formado por una partícula de masa ![]() en una caja en tres dimensiones,
en una caja en tres dimensiones,
![]() ,
, ![]() y
y ![]() , tales que
, tales que ![]() y
y ![]() .
.
- Dibuja un diagrama de niveles de energía para el sistema, en unidades de
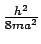 , para los 4 primeros niveles energéticos, indicando su
degeneración.
, para los 4 primeros niveles energéticos, indicando su
degeneración.
- Escribe la función de onda del estado fundamental.
- Si la partícula es un electrón y
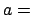 1 Å, calcula la longitud de onda y
el número de ondas para la transición desde el estado fundamental hasta el
primer estado excitado del sistema.
1 Å, calcula la longitud de onda y
el número de ondas para la transición desde el estado fundamental hasta el
primer estado excitado del sistema.
Dada la función de onda siguiente para un átomo de hidrógeno

- Determina, de manera razonada, los números cúanticos que caracterizan la función. ¿De qué orbital de trata?
- Escribe la energía de este estado en función de constantes fundamentales
(
 ,
, 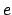 ,
, 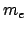 ,...).
,...).
- Halla los máximos y mínimos de la función de distribución radial para ese estado.
- Obtén el valor esperado
de
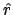 para el átomo en ese estado.
para el átomo en ese estado.
Sea un átomo de Be
- Escribe la configuración electrónica del estado fundamental y la del primer estado excitado.
- Escribe una función de onda aproximada válida para el estado fundamental y otra para el primer estado excitado del sistema.
- Escribe el hamiltoniano electrostático no relativista del sistema.
- Halla los términos espectrales a los que dan lugar cada una de las configuraciones electrónicas e indica cúal de ellos es el de menor energía en cada caso.
Datos