La función de onda del estado fundamental de un oscilador armónico de masa ![]() y constante de fuerza
y constante de fuerza ![]() es
es
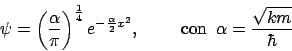
- Esboza la gráfica de las funciones
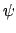 y
y 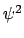 , junto con la curva de potencial del
sistema,
, junto con la curva de potencial del
sistema,
 .
.
- Comprueba que la función de onda está normalizada.
- Calcula el valor medio de
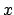 .
.
- Calcula, en función de
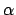 , el valor o los valores de
, el valor o los valores de 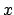 correspondientes a
máximos de la densidad de probabilidad.
correspondientes a
máximos de la densidad de probabilidad.
Un electrón se encuentra en un estado estacionario del átomo de hidrógeno descrito por
el siguiente orbital:
donde la constante de normalización vale
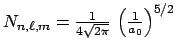
- Comprueba que la constante de normalización
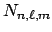 es correcta.
es correcta.
- Calcula el valor más probable de la distancia electrón-núcleo,
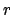 .
.
- Calcula el valor medio de la distancia electrón-núcleo,
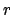 .
.
- Calcula los nodos radiales y angulares que tenga.
- Obtén los valores de los números cuánticos
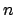 ,
, 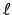 y
y 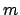 y di de qué orbital se trata.
y di de qué orbital se trata.
Sea una caja de potencial cuadrada de lado
![]() en cuyo interior se encuentra un
electrón. Sabiendo que la función de onda de una partícula en una caja
monodimensional es
en cuyo interior se encuentra un
electrón. Sabiendo que la función de onda de una partícula en una caja
monodimensional es
y que la energía correspondiente es
responde a las siguientes cuestiones para la caja cuadrada:
- Escribe la función de onda normalizada para el estado fundamental del sistema.
- Calcula la energía del estado fundamental.
- Calcula la energía del primer estado excitado y la degeneración de ese nivel de energía.
- Escribe la función de onda de los estados cuya energía corresponde a la calculada en el apartado anterior.
- Calcula el número de ondas (en cm
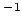 ) de la luz capaz de producir
en el sistema una transición del estado fundamental al primer estado excitado.
) de la luz capaz de producir
en el sistema una transición del estado fundamental al primer estado excitado.