Examen de problemas de Septiembre de 2004.

1. [2 puntos]
   

   El estado fundamental del ion hidrogenoide Li$^{2+}$ se puede representar mediante el orbital
   

   $$\psi = \frac{1}{\sqrt{\pi}} \, \alpha^{3/2}\, e^{-\alpha r}$$
   
   
   1. Demostrad que para que 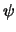$\psi$ sea autofunción (función propia) del operador Hamiltoniano del Li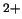$^{2+}$, el valor de 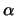$\alpha$ debe ser 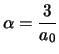$\alpha = {\displaystyle \frac{3}{a_0}}$, donde $a_0 = {\displaystyle \frac{4 \pi \epsilon_0 \hbar^2}{e^2 m}}$.
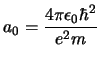   2. Calculad el valor medio (o promedio) de 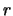$r$ y de la energía potencial $V$ del sistema en dicho estado.
   3. ¿Cuánto vale el módulo del momento angular en dicho estado?
   
   
   
   
   $$\int^{\infty}_0 r^{n} e^{-\beta r} \ dr = \frac{n!}{\beta^{n... ... \frac{\partial}{\partial r} \right) + \frac{\hat{L}^2}{2mr^2}$$
   
   
   
   
   
2. [2 puntos]
   

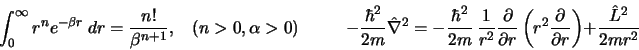
   La función de onda de un estado estacionario de un oscilador armónico monodimensional es:
   

   $$\Psi(x) = \left( \frac{4\alpha^3}{\pi} \right)^{1/4} \, x \,... ... \ \ \ \ \ \ \ \ \ \ \ \ \alpha = \sqrt{\frac{k \mu}{\hbar^2}}$$
   
   
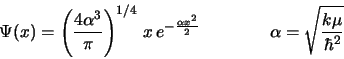
   siendo $k$ la constante de fuerza del oscilador y $\mu$ la masa reducida del sistema.
   1. Comprobad que la función 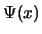$\Psi(x)$ está normalizada.
   2. Hallad los nodos de la función.
   3. Hallad los máximos de la función densidad de probabilidad.
   4. Hallad la probabilidad de encontrar a la partícula entre 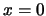$x=0$ y $x=\infty$.
   
   
   
   
   $$\int^{\infty}_{-\infty} x^{2} e^{-\beta x^{2}} \ dx = \frac{1}{2} \, \left( \frac{\pi}{\beta^3}\right)^{1/2}$$
   
   

   
   
   

3. [2 puntos]
   

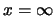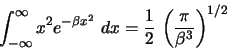
   Una caja cúbica de lado 2 Å contiene 8 electrones.

   1. Calculad la energía, longitud de onda y número de onda correspondientes a la transición entre el estado fundamental y el primer estado excitado del sistema.
   2. Repetid el problema para la misma caja pero conteniendo únicamente un electrón.

   
   
   $m_e$ = 9.11 $\times$ 10$^{-31}$ kg $h$ = 6.63 $\times$ 10$^{-34}$ J$\cdot$s
   $c$ = 3.00 $\times$ 10$^{8}$ m/s 1 Å= 10$^{-10}$ m