Un electrón se encuentra en una caja monodimensional de longitud
- Calculad el valor de la longitud de la caja,
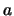 , en Å.
, en Å.
- El estado fundamental de dicho electrón está descrito por la
función de onda
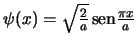 ,
con (
,
con (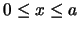 ).
Comprobad que es una solución de la ecuación de Schrödinger
independiente del tiempo.
).
Comprobad que es una solución de la ecuación de Schrödinger
independiente del tiempo.
- Comprobad que la función de onda del apartado anterior está normalizada.
- Calculad la probabiliad de encontrar al electrón en el intervalo
(
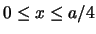 ) cuando está en su estado fundamental.
) cuando está en su estado fundamental.
[
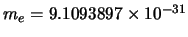 kg,
kg,
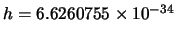 J s,
J s,
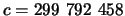 m s
m s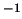 ,
1 m
,
1 m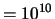 Å
]
Å
]
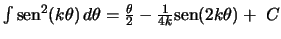
Un electrón se encuentra en un estado estacionario del átomo de hidrógeno descrito por el siguiente orbital:
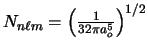
- Comprobad que la constante de normalización es correcta.
- Calculad el valor medio de la distancia electrón-núcleo.
- Calculad el valor medio de la energía potencial.
- Calculad los nodos radiales y angulares que tenga.
- Obtened los números cuánticos
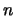 ,
, 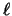 y
y 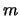 y decid de qué orbital se trata.
y decid de qué orbital se trata.
Elige una de entre las dos preguntas siguientes:
- Muestra que el principio de indeterminación de Heisenberg está contenido
en la ecuación de Schrödinger,
utilizando el estado fundamental y el primer estado excitado de una
partícula en una caja monodimensional de longitud
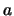 .
.
- Obtén el término espectral más estable de los átomos siguientes
y di cuál es su degeneración:
- El átomo de Na en su configuración
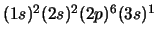 .
.
- El átomo de F en su configuración
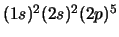 .
.
- El átomo de Be en su configuración excitada
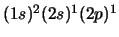 .
.
- El átomo de Sc en su configuración
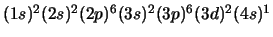 .
.
- El átomo de Na en su configuración
La primera versión de este examen fue escrita en html por José Luis García de Paz. Departamento de Química Física Aplicada, C-XIV-602. e-mail: depaz@uam.es
© Copyright. Noemí Fernández 2003-02-28