Fundamentos de Química Cuántica$1^o$ Química
Examen de septiembre 2002: Problemas y 20% específico

$\hat{\nabla}^2$ = $\frac{1}{r^2}\frac{\partial}{\partial r} \left( r^2 \frac{\partial}{\partial... ...ght) + \frac{1}{r^2 \mbox{sen}^2 \theta} \frac{\partial^2}{\partial \phi^2}$

$\int_0^\infty e^{-\alpha x^2} \,dx = \frac{1}{2} \left( \frac{\pi}{\alpha} \right)^\frac{1}{2}$

$a_o = \frac{\hbar^2}{m_e\,{e^\prime}^2} = \frac{\hbar^2\,4\pi\epsilon_o}{m_e\,e^2} = 0.529 \mbox{\AA}$

1. [2 puntos]
   El estado fundamental del He$^+$ se puede representar mediante el orbital normalizado:
   
   $$\psi = \left( \frac{\alpha^3}{\pi} \right)^\frac{1}{2} \; e^{-\alpha\,r}\,$$
   
   

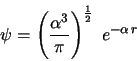
   (a)  Comprobad que para que $\psi$ sea autofunción del hamiltoniano es necesario que el parámetro $\alpha$ tome el valor $\alpha=\frac{Z}{a_o}$.
   (b)  Calculad el valor medio de la distancia electrón-núcleo en dicho estado.
   (c)  Calculad el valor medio de la energía potencial en dicho estado.
   (d)  ¿Cuánto vale el módulo del momento angular en dicho estado?

   
   
   

2. [2 puntos]
   La función de onda de un estado estacionario de un oscilador armónico monodimensional es:
   
   $$\psi = N \, e^{-\frac{\alpha}{2}\,x^2}$$
   
   

   (a)  Calculad la constante de normalización.
   (b)  Encontrad los nodos de esta función.
   (c)  Encontrad los valores de $x$ en los que su densidad de probabilidad es máxima.
   (d)  Calculad la probabilidad de que $x$ este comprendida entre $x=0$ y $x=\infty$

   
   
   

3. [2 puntos]
   Responda brevemente a las siguientes preguntas:

   (a)  Para el átomo de Berilio, escriba la configuración electrónica correspondiente al estado fundamental y deduzca, a partir de ella, cuál es el termino espectral de menor energía.
   (b)  Para el átomo de Berilio, escriba la configuración electrónica correspondiente al primer estado excitado y deduzca, a partir de ella, cuál es el termino espectral de menor energía.
   (c)  Proponga una función de onda electrónica aceptable para describir, de forma aproximada, el estado fundamental del átomo de Berilio.