La función de onda del primer estado excitado de un oscilador armónico de masa
- Comprobad que la constante de normalización vale
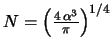 .
.
- Calculad el valor medio de
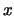 .
.
- Calculad, en función de
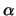 , el valor o los valores
de
, el valor o los valores
de 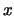 correspondientes a
máximos de la densidad de probabilidad.
correspondientes a
máximos de la densidad de probabilidad.
Dado el siguiente orbital del átomo de hidrógeno:
- Encontrad sus números cuánticos.
- ¿Cuánto valen el módulo y la componente z del momento angular orbital del electrón cuando está en este estado?
- Calculad el valor más probable de la distancia entre el electrón y el núcleo.
- Calculad la probabilidad de hallar el electrón
entre los valores de
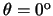 y
y
 .
.