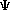Examen de Problemas de Junio de 1999.

1. Una partícula de masa m está sometida a un potencial monodimensional que se anula en la región 0 < x < a y es infinito en cualquier otro punto. Esta partícula se encuentra en un estado descrito por la función de onda:
           (x) = N [ sen ( x/a) + sen (2 x/a)]     con 0 < x < a
   a) Normalizar esta función de onda y obtener la densidad de probabilidad en el punto x = a/2 .
   b) Demostrar si esta función es o no solución de la ecuación de Schrödinger independiente del tiempo.
   
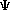2. La función de onda normalizada del orbital hidrogenoide 2s es:
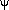           (r,,)_2s = (Z³/(32 a_o³)^1/2 (2 -(Zr/(2a_o))) e^-Zr/(2a_o)
   con a_o = 5.2918x10^-11 m.
   a) Encontrar a qué distancia r_o se anula la densidad de probabilidad para los iones He⁺ y Li²⁺.
   b) Para el ión He⁺ determinar los máximos de la función de distribución radial. Representar dicha función de distribución radial en función de la distancia del electrón al núcleo.

© Copyright.