Examen de Problemas de Junio de 1998.

1. Una partícula de masa m se encuentra en una caja bidimensional de potencial infinito de lados a y b (b=2a).
   a) Escribir las soluciones de la ecuación de Schrödinger independientes del tiempo para dicha partícula y normalizar estas funciones.
   b) Sustituyendo en la ecuación de Schrödinger las funciones obtenidas en (a), calcular la energía del estado fundamental y del primer estado excitado.
   c) Para el estado fundamental, calcular la probabilidad de encontrar la partícula en el rectángulo 0 < x < a/2 ; 0 < y < b/2 .
   Datos: Las soluciones sin normalizar de la ecuación de Schrödinger independiente del tiempo para una partícula en una caja de potencial monodimensional de longitud d tienen la forma:
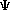           (x) = N sen (n x/d)     con 0 < x < d    y n= 1,2,3,..
   
2. La función de onda de un orbital del átomo de hidrógeno es:
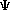       = [ 1/(32  a_o⁵) ]^1/2 . r . e ^-r/2a_o . sen  . sen 
   con a_o = 5.2918x10^-11m. Se pide:
   a) Decir de qué orbital se trata. Evaluar la función de onda y la densidad de probabilidad en los puntos de coordenadas (x=0, y=a_o, z=0) y (x=0, y=-a_o, z=0).
   b) Encontrar el máximo de la correspondiente función de distribución radial.

© Copyright.