- a)
- Dada la función de onda
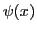 representada en la siguiente figura, indicad a qué estado
estacionario
representada en la siguiente figura, indicad a qué estado
estacionario 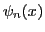 representa. Razonadlo brevemente.
representa. Razonadlo brevemente.
![\includegraphics[scale=0.45 angle=-90]{fig24.ps}](img7.gif)
- b)
- Determinad los valores medios de la energía cinética y energía potencial para el caso general y a partir de ellas obtened el valor medio de la energía total.
- c)
- Obtened el valor de la función de onda y de la densidad de probabilidad en los puntos
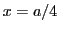 y
y 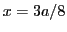 .
.
- a)
- Si el estado del sistema es tal que la energía vale
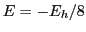 y la componente
y la componente  del momento angular vale
del momento angular vale
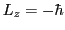 , indicad razonadamente de qué estado se trata.
, indicad razonadamente de qué estado se trata.
Sabiendo que la función de onda es de la forma:
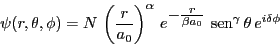
indicad los valores de y relacionarlos con los números cuánticos.
y relacionarlos con los números cuánticos.
- b)
- Dado el siguiente orbital del átomo de hidrógeno
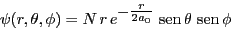
Comprobad que la constante de normalización vale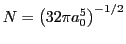 .
.
- c)
- Calculad, para el caso del apartado b), el valor más probable de la distancia electrón-núcleo.
- 3a.
- La medida del efecto fotoeléctrico en una muestra de metal de cobre produjo
el siguiente resultado:
![\includegraphics[width=7cm]{efecto_fotoelectrico.ps}](img18.gif)
El ajuste por mínimos cuadrados a los datos experimentales da una recta de pendiente
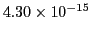 eV/Hz y una frecuencia umbral de
eV/Hz y una frecuencia umbral de
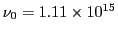 Hz.
Hz.
- a)
- Explicad muy brevemente por qué no se observan electrones cuando
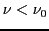
- b)
- Calculad la constante de Planck.
- c)
- Calculad la función de trabajo del cobre.
- 3b.
- Obtened los términos espectrales que se obtienen para el átomo de Silicio en la siguiente configuración
electrónica
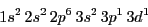
y ordenadlas de menor a mayor energía aplicando las reglas de Hund.
Datos:
![]() = 1.6022
= 1.6022
![]() C,
C,
![]() 2.9979
2.9979 ![]() m s
m s![]() ,
,
![]() 6.6261
6.6261
![]() J s
J s