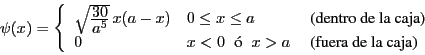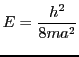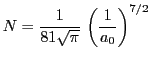Fundamentos de Química Cuántica
1 de Ciencias Químicas
de Ciencias Químicas
Examen 15 de junio de 2007 (problemas)
- Considerar la siguiente función de onda aproximada para una partícula de masa
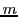 en una
caja monodimensional de longitud
en una
caja monodimensional de longitud 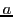 :
:
- Comprobar que es una función de onda aceptable.
- Comprobar que dicha función de onda está normalizada.
- Determinar el valor medio de la posición
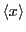 .
.
- Determinar el valor medio de la energía
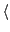 E
E y comparadlo
con el valor exacto para la energía del estado fundamental
y comparadlo
con el valor exacto para la energía del estado fundamental
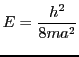
- Un electrón se encuentra en un estado estacionario del átomo de hidrógeno descrito por el
siguiente orbital:
donde la constante de normalización vale
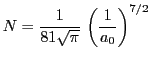
- Obtener razonadamente los valores de los números cuánticos
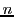 ,
, 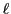 y
y 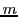 e indicar de
qué orbital se trata.
e indicar de
qué orbital se trata.
- Calcular el valor más probable de la distancia electrón-núcleo,
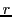 .
.
- Calcular los nodos radiales de la función de onda, indicando los valores de
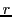 correspondientes.
correspondientes.
- Calcular los nodos angulares de la función de onda, indicando los valores de
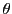 y
y 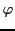 correspondientes.
correspondientes.
- Responder brevemente a las siguientes preguntas:
- Para el átomo de carbono, escribir la configuración electrónica correspondiente al
estado fundamental y deducir, a partir de ella, los términos espectrales. Ordenar
dichos términos por energía aplicando las reglas de Hund.
- Para el catión C
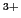 , escribir una función de onda electrónica aceptable
para describir, de forma aproximada, el estado fundamental del catión C
, escribir una función de onda electrónica aceptable
para describir, de forma aproximada, el estado fundamental del catión C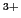 .
.
2008-07-02
![]() de Ciencias Químicas
de Ciencias Químicas