Sea, para una caja de potencial de una dimensión (![]() ), la siguiente función de
onda aproximada
), la siguiente función de
onda aproximada
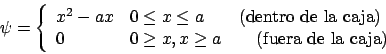
- Comprobad que es una función de onda aceptable (o sea, bien comportada).
- Normalizad la función
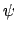 .
.
- Comprobad si
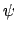 es una función propia del hamiltoniano del sistema.
es una función propia del hamiltoniano del sistema.
- Determinad
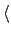 E
E y comparad con el valor exacto para
la energía del estado fundamental
y comparad con el valor exacto para
la energía del estado fundamental
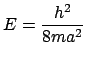 .
.
La función de onda del segundo estado excitado de un oscilador armónico monodimensional
es:
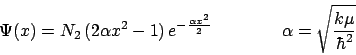
siendo
- Comprobad que la constante de normalización
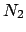 vale
vale
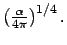
- Hallad
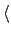 x
x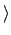 .
.
- Determinad los puntos de retorno clásicos del oscilador en el estado
dado arriba, expresando el resultado en función de
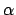
- Determinad la posición de los nodos de
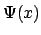 .
.
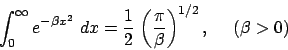
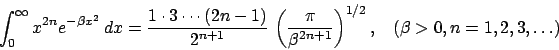
Sea un ion He![]() en un estado descrito por la función
en un estado descrito por la función
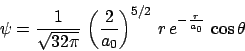
- Determina los números cuánticos de la función.
- Escribe la energía de este estado en función de constantes
fundamentales (e, m
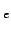 , h, a
, h, a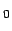 ...)
...)
- Calculad el valor medio (o promedio) de energía potencial
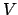 del sistema en dicho estado.
del sistema en dicho estado.
- Determinad la posición de los máximos y mínimos de la función de distribución radial.