La función de onda del primer estado excitado de un oscilador armónico de masa ![]() y constante de fuerza
y constante de fuerza ![]() es
es
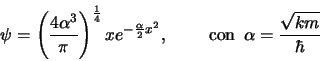
- Esboza la gráfica de las funciones
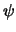 y
y 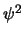 .
.
- Calcula el valor medio de
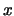 .
.
- Calcula, en función de
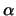 , el valor o los valores de
, el valor o los valores de 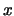 correspondientes a
máximos de la densidad de probabilidad.
correspondientes a
máximos de la densidad de probabilidad.
Dada la función de onda 2![]() para un átomo hidrogenoide de carga núclear
para un átomo hidrogenoide de carga núclear ![]()
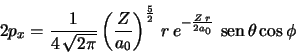
- Calcula el valor más probable de la distancia electrón-núcleo,
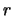 .
.
- Compara los resultados para H, He
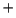 y Li
y Li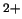 .
.
- Discute si la función 2
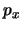 es autofunción del operador
es autofunción del operador
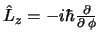 y obtén el valor esperado
de
y obtén el valor esperado
de 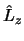 para un átomo de H descrito por esta función.
para un átomo de H descrito por esta función.
Una partícula de masa ![]() se encuentra confinada en una caja rectangular
de lados
se encuentra confinada en una caja rectangular
de lados ![]() y
y ![]() con
con
![]() .
.
- Escribe la expresión general de las funciones de onda bien comportadas que cumplen la ecuación de Schrödinger y la expresión correspondiente a los niveles energéticos del sistema.
- Haz un diagrama mostrando los cinco niveles energéticos de menor energía e indicando su degeneración.
- Si la partícula es un electrón y
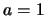 Å, calcula la
longitud de onda
Å, calcula la
longitud de onda 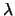 (en Å) de la transición desde el estado
fundamental del sistema hasta el segundo estado excitado.
(en Å) de la transición desde el estado
fundamental del sistema hasta el segundo estado excitado.