Examen de Problemas de junio de 2004.

1. [2 puntos]
   

   Una partícula se encuentra en una caja cúbica de lados $a$, $b$ y $c$, con $b = a$ y $c=2a$.

   1. Escribid la expresión general de las funciones de onda bien comportadas para este sistema.
   2. Hallad la expresión correspondiente a los niveles de energía del sistema. Dibujad un diagrama que represente los tres niveles más bajos, indicando su degeneración.
   3. Si la partícula es un electrón y 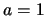$a = 1$ Å, calculad la frecuencia y la longitud de onda de la transición desde el estado fundamental del sistema hasta el segundo estado excitado.
   
   
   $m_e$ = 9.11 $\times$ 10$^{-31}$ kg $h$ = 6.63 $\times$ 10$^{-34}$ J$\cdot$s
   $c$ = 3.00 $\times$ 10$^{8}$ m/s 1 Å= 10$^{-10}$ m
   
   
2. [2 puntos]
   

   Un electrón se encuentra en un estado estacionario del átomo de hidrógeno descrito por el siguiente orbital:
   

   $$\psi_{n,\ell,m} = N_{n,\ell,m} \, r\, e^{-\frac{r}{2a_0}} \, \cos{\theta}$$
   
   
   donde la constante de normalización vale $N_{n,\ell,m} = \frac{1}{4\sqrt{2 \pi}} \, \left(\frac{1}{a_0}\right)^{5/2}$
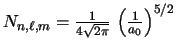
   1. Comprobad que la constante de normalización 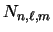$N_{n,\ell,m}$ es correcta.
   2. Calculad el valor más probable de la distancia electrón-núcleo, $r$.
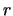   3. Calculad el valor medio de la distancia electrón-núcleo, $r$.
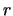   4. Calculad los nodos radiales y angulares que tenga.
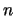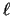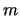   5. Obtened los valores de los números cuánticos $n$, $\ell$ y $m$ y decid de qué orbital se trata.
   
   
   
   
   $$\int^{\infty}_0 r^{n} e^{-\alpha r} \ dr = \frac{n!}{\alpha^{n+1}}, \ \ \ \ (n>0, \alpha >0)$$
   
   

   
   
   

3. [2 puntos]
   
   1. Para el átomo de Li en su estado fundamental

      a1.

      Escribid su hamiltoniano.

      a2.

      Escribid una función de onda que represente correctamente al átomo con una configuración electrónica $(1s)^2 (2s)^1$.

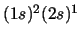      a3.

      Obtened los términos espectrales permitidos para esa configuración.

   2. Para los átomos de Be en su configuración excitada 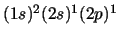$(1s)^2 (2s)^1 (2p)^1$ y de C en su configuración excitada $(1s)^2 (2s)^2 (2p)^1 (3d)^1$.

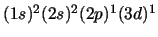      b1.

      Obtened todos los términos espectrales permitidos.

      b2.

      Ordenad estos términos por orden creciente de energías usando las reglas de Hund.