Un oscilador armónico de masa efectiva
- Comprobad que la constante de normalización vale
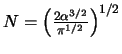
- Calculad el valor medio de la energía potencial en ese estado,
expresándola en función de
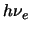 .
.
- Calculad el valor medio de la energía cinética en ese estado,
expresándola en función de
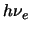 .
.
- Calculad el valor de la densidad de probabilidad en los puntos en los que
toma su valor máximo,
expresándola en función de
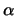 .
.
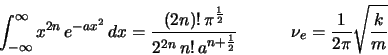
Un electrón se encuentra en un estado estacionario del átomo de hidrógeno descrito por el siguiente orbital:
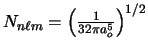
- Comprobad que la constante de normalización es correcta.
- Calculad el valor más probable de la distancia electrón-núcleo.
- Calculad el valor medio de la distancia electrón-núcleo.
- Calculad los nodos radiales y angulares que tenga.
- Obtened los números cuánticos
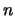 ,
, 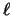 y
y 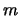 y decid de qué orbital se trata.
y decid de qué orbital se trata.
Elige una de entre las dos preguntas siguientes:
- Sabiendo que la solución general de una ecuación diferencial del tipo
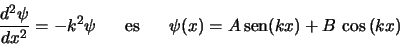
obtén las funciones de onda y las energías de los estados estacionarios de una partícula en una caja monodimensional de longitud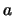 .
.
- Obtén el término espectral más estable de los átomos siguientes
y di cuál es su degeneración:
- El átomo de Mg en su configuración
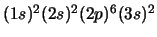 .
.
- El átomo de O en su configuración
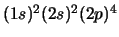 .
.
- El átomo de C en su configuración excitada
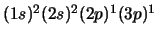 .
.
- El átomo de Ti en su configuración
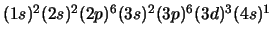 .
.
- El átomo de Mg en su configuración