Fundamentos de Química Cuántica$1^o$ Química
Examen de junio 2002: Problemas y 20% específico

$\int \mbox{sen}^2 (kx) \,dx = \frac{x}{2} - \frac{1}{4k} \mbox{sen} (2kx) + C$

$\int \mbox{cos}^2 (kx) \,dx = \frac{x}{2} + \frac{1}{4k} \mbox{sen} (2kx) + C$

$\int \mbox{sen}^3 (kx) \,dx = -\frac{\mbox{cos} (kx)}{3k} \left[ \mbox{sen}^2 (kx) + 2 \right] + C$

$\int_0^{\infty} r^n e^{-\alpha\,r} \,dr = \frac{n!}{\alpha^{n+1}}$

$a_o = \frac{\hbar^2}{m_e\,{e^\prime}^2} = \frac{\hbar^2\,4\pi\epsilon_o}{m_e\,e^2} = 0.529 \mbox{\AA}$

1. [2 puntos]
   Una partícula en una caja monodimensional de longitud $a$ se encuentra en un estado estacionario cuya función de onda independiente del tiempo viene dada por:
   
   $$\psi(x) = \left( \frac{2}{a} \right)^{1/2} \,\, \mbox{sen}~\frac{3 \pi x}{a} \,, \,\,\,\,\,\,\,\,(0\leq x \leq a).$$
   
   

   (a)  Comprobad que dicha función de onda está normalizada.
   (b)  Calculad la probabilidad de que la partícula se encuentre entre $0 \leq x \leq \frac{a}{3}$.
   (c)  Calculad la energía de este estado por sustitución en la ecuación de Schrödinger independiente del tiempo.

   
   
   

2. [2 puntos]
   Dada la función de onda normalizada $2p_x$ de un átomo o ion hidrogenoide de carga nuclear $Z$:

   
   

   $$2p_x = \frac{1}{4\sqrt{2\pi}} \; \left(\frac{Z}{a_o}\right)^... ...rac{Z\,r}{2\,a_o}} \; \mbox{sen}~\theta \; \mbox{cos}~\varphi$$
   
   

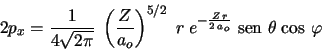
   (a)  Calculad el valor medio de la distancia electrón-núcleo.
   (b)  Calculad el valor más probable de la distancia electrón-núcleo.
   (c)  Comparad los valores anteriores en los casos del H, del He$^+$ y del Li$^{2+}$.

   
   
   

3. [2 puntos]
   En la figura A se representa la superficie de energía potencial (en eV) para la reacción colineal $A+BC \rightarrow AB+ C$.

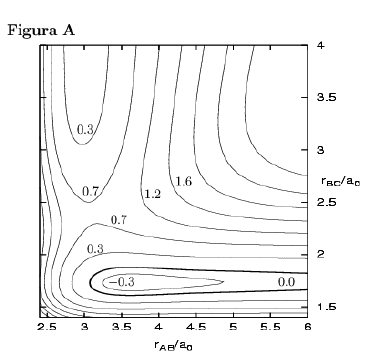
   (a)  Indicad, sobre la figura A, cuáles son los reactivos, productos, punto silla (estado de transición) y mínimos.

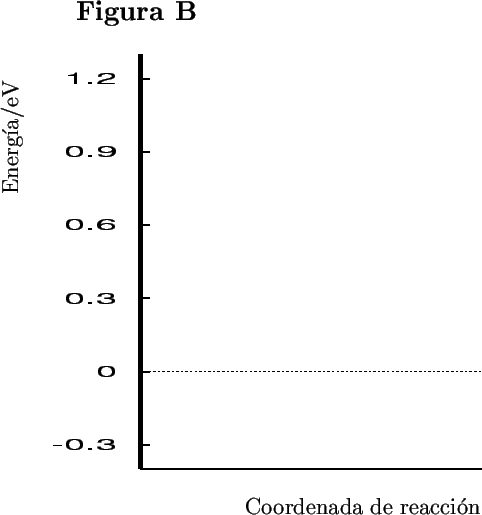
   (b)  Haced un dibujo cualitativo del camino de mínima energía sobre la figura A, y representad cualitativamente la variación de la energía con la coordenada de reacción en la figura B.

   (c)  Indicad, justificando brevemente la respuesta, si la reacción es endotérmica o exotérmica.