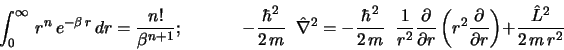Una partícula de masa
- Escribid las soluciones bien comportadas de la Ecuación de Schrödinger.
- Hallad la expresión correspondiente de los niveles energéticos del sistema.
- Si la partícula es un electrón y
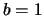 Å,
calculad la frecuencia,
Å,
calculad la frecuencia, 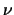 , y la longitud de onda,
, y la longitud de onda, 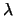 ,
de la transición desde el primer nivel excitado hasta el segundo
nivel excitado del sistema.
,
de la transición desde el primer nivel excitado hasta el segundo
nivel excitado del sistema.
El estado fundamental del ion hidrogenoide Be
- Demostrad que para que
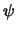 sea autofunción (función propia)
del operador Hamiltoniano del Be
sea autofunción (función propia)
del operador Hamiltoniano del Be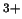 ,
el valor de
,
el valor de 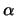 debe ser
debe ser 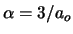 .
.
- Calculad los valores medios (o promedio) de
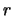 y de la energía
potencial
y de la energía
potencial 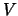 en dicho estado.
en dicho estado.
- ¿Cuánto vale el momento angular en dicho estado?