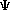Examen de Problemas de Junio de 2000.

1. La función de onda para un orbital del átomo de hidrógeno es:
           = N r e^{-r/(2 a_o)} cos      Se pide:
   a) Encontrar sus números cuánticos.
   b) Comprobar que la constante de normalización vale
           N = (1/(32 a_o⁵))^1/2
   c) Encontrar el valor del radio más probable (valor en que la función de distribución radial es máximo).
   d) Encontrar la probabilidad de hallar el electrón entre los valores de r=0 y r=a_o.
   
2. Sea una caja de potencial cuadrada de lado a = 1 Angstrom en cuyo interior se encuentra un electrón. Sabiendo que la energía de una caja monodimensional corresponde a E_n = n² h²/(8ma²) y la función de onda de la caja monodimensional es
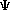           _n(x) = (2/a)^1/2 sen (n x/a)
   Para la caja de potencial cuadrada se pide:
   a) Escribir la función de onda del estado fundamental normalizada.
   b) Encontrar la energía del estado fundamental.
   c) Encontrar la energía del primer estado excitado y su grado de degeneración.
   d) Escribir las funciones de onda del primer estado excitado normalizadas.
   e) Calcular el número de onda (cm^-1) correspondiente a la luz capaz de producir en el sistema una transición del estado fundamental al primer estado excitado.

© Copyright.