Experiencia Piloto de Evaluación Continuada para la Asignatura de “Fundamentos de la Química Cuántica” de 1º de Ciencias Químicas.

Curso 2005/06

Segundo Ejercicio: Se enunciará el 20 de abril y se entregará al profesor hasta el 4 de mayo. Se pueden presentar hechos con ordenador únicamente los gráficos y figuras.

Haz bibliografía para saber cuanto valen las constantes y datos que necesites para resolver el problema que se te propone a continuación, tales como, por ejemplo, la masa del protón, masa de los isótopos, la constante de Planck, la velocidad de la luz, integrales resueltas que necesites, etc. Indica el título, autores y página de los libros (o revistas científicas) de dónde hayas obtenido estos datos. Realiza las operaciones y ajustes que necesites teniendo en cuenta las cifras significativas.

1. Un protón se mueve en la dirección X alrededor de x=0 sujeto a un potencial de oscilador armónico V = 1/2 K x² . Plantea la ecuación de Schrödinger para este sistema. Escribe la expresión de la solución en el estado fundamental y en el primer excitado. En el primer estado excitado, calcula los puntos de retorno clásicos (valor de x en que la energía cinética es nula), el valor medio de la posición de la partícula y la posición en que la probabilidad de encontrar la partícula sea máxima. Puedes dejar el resultado en función de la constante 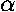que hay en el exponente de la función de onda.

2. Repite el mismo problema pero ahora el protón se encuentra oscilando alrededor de la posición x=2 Angstrom, con el potencial V = 1/2 K (x-2)². Indica las diferencias y similitudes físicas entre los resultados obtenidos.

3. Para el oscilador del apartado 1, indica el valor de la energía del punto cero. Razona porqué no es posible que la partícula pueda estar parada en el estado fundamental del oscilador armónico.

4. Sea un oscilador armónico isótropo en dos dimensiones (K_x = K_y = K) que oscila alrededor del origen de coordenadas. Escribe la expresión de la energía de los estados del sistema, citando la referencia del libro que has empleado. Calcula la longitud de onda y la frecuencia de la radiación que debería absorber el protón para pasar del estado fundamental al segundo estado excitado del sistema. Suponer K = 2000 N/m

5. La banda más intensa del espectro Infrarrojo (correspondiente al movimiento de vibración molecular) del ¹H³⁵Cl aparece a 8.65x10¹³ Hz. Calcula la constante de fuerza del enlace de esta molécula suponiendo que sigue el modelo del oscilador armónico. Obtén la energía vibracional del punto cero para la molécula. Si la constante de fuerza del enlace no cambia con la sustitución de un isótopo por otro en la molécula, calcular la frecuencia y el número de ondas para la banda infrarroja más intensa de la molécula de ²H³⁵Cl.